
Читайте также:
|
Методика ознакомления учащихся начальных классов с понятием дроби. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл частного.
План:
1. Общие вопросы методики ознакомления младших школьников с дробями.
2. Методика ознакомления с долями величины
3. Сравнение дробей
4. Решение задач на нахождение доли числа и числа по его доле
– Доля – это одна часть от целого - 1/5, 1/123
– Дробь – 2 и более частей от целого числа – 2/5, 4/18, 12/100
– Сравнить дробь, это значит найти какой значение надо поставить между двумя дробями <, >, =,
Ознакомить учащихся с понятием доли, значит сформировать у них конкретное представление о долях, т. е. научить детей образовать доли практически.
Для формирования правильных представлений о долях надо использовать достаточное количество разнообразных наглядных пособий. Нам более удобными пособиями являются геометрические фигуры, из бумаги, в форме прямоугольника, круга, треугольника, отрезка и т.д.
Правильное представление о долях, а позднее о дробях будут сформированы тогда, когда ученики своими руками получать, например, половину квадрата, круга, четверть отрезка и т.д.
Доли записываются с помощью двух чисел. Одна вторая доля квадрата обозначается 1/2. Число 2 показывает, что квадрат разделен на 2 равные части, а число 1 показывает, что взяли одну такую часть.
Аналогично получает ¼, 1/6, 1/12. Решение задач на нахождение доли числа и числа по его доле также способствует формированию представлений о долях величины. Потому решение задач на нахождение доли числа и числа по его доле выполняется на наглядной основе.
Образование дробей, как и образование долей рассматривается с помощью наглядных пособий. Для сравнения дробей обычно используются иллюстрации е разными прямоугольниками.
Предлагаются специальныеупражнения на сравнение дробей:
1. Вставьте пропущенный знак
2. Конкретный смысл дроби ярко раскрывается при решении задач на нахождение дроби числа. Решение этих задач, как и задач на нахождение доли числа, выполняется с помощью соответствующих наглядных пособий.
Например, у закройщика было 12 метров ткани. 3:2 всей ткани израсходовал. Сколько метров ткани израсходовал закройщик?
Различные упражнения с дробями следует чаще включать для устных и письменных работ на протяжении всего учебного года.
Дети должны уметь записывать дробь, ориентируясь на объект или рисунок, сравнивать дроби с опорой на объект или рисунок, находить дробь от числа и восстанавливать число по его дроби.
Дети должны уметь сравнивать дроби с опорой на объект или рисунок.
Для сравнения долей используется рисунок круга, разделённый на несколько равных частей.
Методика ознакомления учащихся начальных классов с алгоритмом письменного вычитания. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл разности натуральных чисел.
Алгоритм вычитания:
1. Записывают вычитаемое bп bп-1... b1b0 под уменьшаемым ап ап-1... а 1 а 0так, чтобы соответствующие разряды находились друг под другом.
2. Если цифра в разряде единиц вычитаемого не превосходит соответствующей цифры уменьшаемого, то ее вычитают из соответствующей цифры уменьшаемого, после чего переходят к следующему разряду.
3. Если цифра единиц вычитаемого больше цифры единиц уменьшаемого, т. е. а0 < Ь0, а цифра десятков уменьшаемого отлична от нуля, то уменьшают цифру десятков уменьшаемого на 1, одновременно увеличивают цифру единиц уменьшаемого на 10, после чего вычитают из числа 10+a0 число b0 и записывают результат в разряде единиц разности. Далее переходят к следующему разряду.
4. Если цифра единиц вычитаемого больше цифры единиц уменьшаемого, а цифры, стоящие в разряде десятков, сотен и т. д. уменьшаемого, равны нулю, то берут первую, отличную от нуля цифру в уменьшаемом (после разряда единиц), уменьшают ее на 1, все цифры в младших разрядах до разряда десятков увеличивают на 9, а цифру в разряде единиц — на 10, вычитают Ь0 из 1 0+а0, записывают результат в разряде единиц разности и переходят к следующему разряду.
5. В следующем разряде описанный процесс повторяется.
6. Процесс вычитания заканчивается, когда произведено вычитание из старшего разряда уменьшаемого.
Младшие школьники не могут усвоить алгоритмы вычитания в общем виде. Но учителю знать их необходимо. Это позволит ему:
а) при ознакомлении учащихся с алгоритмом правильно организовать подготовительную работу;
б) управлять деятельностью школьников, направленной на усвоение алгоритма;
в) подбирать и составлять различные задания, нацеленные на усвоение операций, входящих в алгоритмы письменного вычитания.
Описания алгоритмов даются учащимся в упрощенном виде, где фиксируются только основные моменты:
• Вычитаемое нужно записать под уменьшаемым так, чтобы соответствующие разряды находились друг под другом;
• Вычитание следует начинать с низшего разряда, т. е. вычитать сначала единицы.
Для формирования общего способа действий целесообразно познакомить учащихся с алгоритмами письменного вычитания после того, как они усвоят нумерацию чисел в пределах миллиона. При этом их деятельность должна быть направлена не на отработку частных случаев вычитания, а на осознание тех операций, которые входят в алгоритмы. Для этого уже при изучении нумерации полезно обратить внимание детей на то, как изменяется цифра, стоящая в определенном разряде данного числа при его уменьшении на разрядные единицы, десятки, сотни, тысячи и т. д. В процессе этих упражнений дети осознают соотношение разрядов и значение каждой цифры в записи числа. Это способствует сознательному усвоению механизма письменного вычитания.
Необходимо помочь детям овладеть сначала одним способом действия — алгоритмом письменного сложения, а затем другим способом действия — алгоритмом письменного вычитания. Поэтому к знакомству с алгоритмом письменного вычитания следует приступить только после того, как будет усвоен алгоритм письменного сложения.
Задания:
На сколько можно уменьшить число 28746, чтобы изменились цифры, стоящие в разряде единиц и десятков, а цифры в других разрядах остались те же?
Запиши вычитание «в столбик» и выполни вычисления. а) 37836-7417; б)984758-321639
в) 378836-74618 г)465676-35129
3. Методика ознакомления учащихся начальных классов с правилом умножения суммы на число. Примеры тождественных преобразований выражений, выполняемых младшими школьниками при изучении устных приёмов умножения двузначных чисел на однозначные.
Распределительное свойство умножения также целесообразно объяснять на основе приема соотнесения предметных и символических моделей, который создает условия для анализа, сравнения, обобщения и понимания детьми формулировки данного свойства. Предлагаются задания:
Догадайся: что обозначают выражения, записанные под каждым рисунком? Чем они похожи? Чем отличаются? Вычисли их значения.






 а)
а)
 |  |  |  |  |  |  | |||||||
 |  |  |  |  |  |  |
5*3+2*3
(5+2)*3
Сколько всего квадратов в красном и синем прямоугольниках?
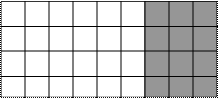 |
Маша ответила на вопрос так:
6*4+3*4=36 (кв.).
Миша — так:
(6+3)*4=36 (кв.).
Как рассуждали Маша и Миша? Кто из них прав?
Главным средством усвоения распределительного свойства умножения также являются учебные задания. Например:
Вставь знаки <, > или =, чтобы получились верные записи:
(14+8)*3 14*3+8*3
(27+8)*6 27*6+8
(36+4)*18 40*18
Вставь пропущенные числа, чтобы равенства были верными:
а) (8+)*3= +4*3
б)(+)*5=35+45
Знакомство школьников с распределительным свойством умножения позволяет им самостоятельно «открыть» рациональный вычислительный прием устного умножения двузначного числа на однозначное, проверять результаты вычислений, используя различные способы, а также находить различные методы решения текстовых задач.
Методика ознакомления учащихся начальных классов с понятием уравнения. Примеры уравнений из учебников математики для начальной школы и способы их решения.
В курсе математики начальных классов уравнение рассматривается как истинное равенство, содержащее неизвестное число, и решается на основе правил взаимосвязи между компонентами и результатами действий.
Термин «решение» употребляется в двух смыслах: он обозначает как число (корень), при подстановке которого уравнение обращается в верное числовое равенство, так и сам процесс отыскания такого числа, т. е. способ решения уравнения.
Приступать к решению уравнений после того, как учащиеся усвоят необходимую терминологию и те правила, которыми они будут пользоваться для решения уравнений. Для осознания взаимосвязи между компонентами и результатами арифметических действий необходимо опираться на предметную деятельность, а овладение терминологией и правилами распределить во времени и связать по возможности с изучением других вопросов курса.
В противном случае при решении уравнений мы вынуждены идти путем действий по образцу, сопровождая их большим количеством тренировочных однообразных упражнений. Это приводит к тому, что, решая уравнения, учащиеся часто руководствуются не общим способом действия (правилом), а внешними признаками.
Например, предложив детям решить уравнение 8+х=6, мы довольно часто получаем ответ: x=8-6, который ребята обосновывают так: «Здесь знак «+», значит, надо вычитать, я из большего числа вычитаю меньшее». Ясно, что дети ориентируются не на существенные признаки данного равенства, а на числа 8 и 6. А так как младший школьник может вычитать только меньшее число из большего, то он и оценивает данное равенство с этой точки зрения, не пытаясь осознать взаимосвязь, которая существует между слагаемыми и значением суммы.
Задания:
1. Запиши каждое предложение уравнением и реши его.
а) Неизвестное число уменьшили на 708 и получили 1200.
б) Число 1208 уменьшили в несколько раз и получили 302.
в) Неизвестное число увеличили в 7 раз и получили 1449.
2. Познакомить учащихся с уравнениями, в которых неизвестный компонент представлен в виде буквенного выражения:
а) 5 -х- 10=290
б)5*(х-10)=290
При решении усложненных уравнений следует опираться на правила порядка выполнения действий, так как не все ученики могут овладеть способом действия при отсутствии четких ориентиров. Порядок действий расставляется в той части уравнения, где содержится неизвестное (х).
5*x-10=290
3. Познакомить детей с решением задач способом составления уравнений. При этом можно возвращаться к тем задачам, которые они решали ранее арифметическим способом. Ребята находят в учебнике задачу, которую они уже решали арифметическим способом (учитель называет номер).
Для подготовки учащихся к решению задач способом составления уравнений полезны задания на соотнесение вербальных, предметных, схематических и символических моделей.
Например:
На одной чашке весов дыня и гиря массой 2кг. На другой — гири массой 10кг и 5кг. Весы находятся в равновесии.
Какое уравнение можно составить по данному рисунку, если масса дыни х кг?
Объясни, почему по данной схеме можно составить уравнение: х+40=56+32. Найди корень уравнения.
Методика ознакомления учащихся начальных классов со свойствами действия сложения. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл суммы натуральных чисел.
Из курса математики вам известно, что для сложения целых неотрицательных чисел используются его коммутативное и ассоциативное свойства. В начальном курсе математики учащиеся знакомятся с коммутативным свойством сложения, называя его «переместительное свойство сложения» или «перестановка слагаемых».
Ассоциативное свойство сложения представлено в курсе математики начальных классов как сочетательное свойство сложения.
Понимание первоклассниками формулировки переместительного свойства сложения («От перестановки слагаемых значение суммы не меняется») требует специальной подготовительной работы, которая включает различные действия с предметными моделями, анализ и сравнение рисунков, а также усвоение необходимой терминологии. Поэтому при формировании у детей представлений о смысле сложения полезно предлагать им такие ситуации для предметных действий, при выполнении которых они сами подмечают закономерность, связанную с переместительным свойством сложения.
Например:
На левой тарелке 4 апельсина, на правой — 3. Покажи, сколько апельсинов на двух тарелках.
Ученики выполняют схематический рисунок и записывают равенство, подсчитав количество апельсинов на двух тарелках.
Теперь на левой тарелке 3 апельсина, на правой — 4. Покажи, сколько апельсинов на двух тарелках.
Ученики выполняют схематический рисунок и записывают равенство, подсчитав количество апельсинов на двух тарелках.
|О О О О||О О О| 4+3=7
|О О О|| О О О О| 3+4=7
Сравнивая рисунки (в чем их сходство и различие), дети убеждаются в том, что количество апельсинов на двух тарелках не изменилось.
Анализ предметных моделей и их соотнесение с математическими записями — важное условие для понимания учащимися формулировки переместительного свойства сложения.
С сочетательным свойством сложения младших школьников целесообразно познакомить при изучении табличных случаев сложения однозначных чисел с переходом в другой разряд (7+6, 9+5, 8+4 и т. д.).
Если действия с сочетательным свойством сложения предшествуют составлению таблицы сложения в пределах 20, то необходимо так же, как и при работе с переместительным свойством сложения, использовать соотнесение предметных и символических моделей. В этом случае сочетательное свойство сложения послужит теоретической основой вычислительного приема при сложении однозначных чисел с переходом в другой разряд.
Однако, обращение к «теоретическим основам» того или иного вычислительного приема для большинства младших школьников представляет определенную трудность, преодоление которой требует воспроизводящей деятельности и заучивания образцов рассуждений. Использование же предметных моделей (десятков и единиц) позволяет детям «открыть» тот или иной вычислительный прием самостоятельно. В этом случае, знакомство с сочетательным свойством сложения выступает как содержательный материал для развития мышления учащихся. Дети сами «открывают» сочетательное свойство сложения, пользуясь приемами анализа и синтеза, сравнения и обобщения.
Для этой цели можно воспользоваться, например, таким заданием:
Догадайся, по какому правилу записаны равенства слева и справа, и вставь числа в «окошки»:
9+1+6=10+6 9+1+6=9+7
8+2+4=10+4 8+2+4=8+6
7+3+2=10+2 7+3+2=7+5
Какое правило ты заметил?
Возникает необходимость введения нового математического знака (скобок). С их помощью можно записать высказывания школьников в таком виде: (9+1)+6=9+(1+6) (8+2)+4=8+(2+4)
и сформулировать сочетательное свойство сложения: «Два соседних слагаемых можно заменить значением суммы». Скобки же в данном случае показывают, какое действие следует выполнять первым.
Методика ознакомления учащихся начальных классов с понятием числовых равенств и неравенств. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл натурального числа.
Пусть а и в - числовые выражения. Числовые выражения или числа, между которыми стоит знак равенства, называются числовыми равенствами.
Неравенство - отношение, связывающее два числовые выражения или два числа посредством одного из знаков ”>” (больше), ”<” (меньше), ”” (больше или равно), ”” (меньше или равно), (не равно).
Для установления между числами отношений «больше», «меньше», «равно» младшие школьники могут использовать предметные, графические и символические модели.
Предметные модели удобны для определения взаимно-однозначного соответствия, когда каждый предмет одной совокупности соединяется с одним предметом другой совокупности (образование пар).
Функции графической модели выполняет числовой луч, с которым учащихся целесообразно познакомить в первом классе. Естественно, что введению числового луча должно предшествовать знакомство с лучом и отрезком.
Построение числового луча полезно выполнять не только в тетрадях, где, выбирая единичный отрезок (мерку), первоклассники ориентируются на клетки, но и на белом листе бумаги, располагая по-разному луч и выбирая различные мерки (единичные отрезки). В этом случае дети пользуются циркулем.
Нумеруя на числовом луче отложенные отрезки (мерки) и соотнося конец каждого с определенным числом, ребята убеждаются, что если двигаться вправо по числовому лучу, то числа увеличиваются, а если двигаться влево, то числа уменьшаются. Следовательно, числовой луч можно использовать и для сравнения чисел.
Чтобы ученики могли записывать отношения между числами, учитель знакомит их со знаками > (больше), < (меньше), = (равно) и с математическими записями, которые называются равенствами и неравенствами (5<9, 9>5, 5=5).
В качестве символической модели используется отрезок натурального ряда (ряд чисел, которым можно пользоваться при счете предметов: «5<9, так как число 5 называется при счете раньше, чем 9»).
Графической моделью служит числовой луч, на котором дети отмечают точки, соответствующие натуральным числам.
Методика ознакомления учащихся начальных классов с действием вычитания. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл разности натуральных чисел.
При формировании у первоклассников представлений о вычитании можно условно ориентироваться на следующие предметные ситуации:
а) уменьшение данного предметного множества на несколько предметов (предметы, которые удаляются, зачеркиваются).
Пример: «У Маши было шесть шаров. Два она подарила Тане. Покажи шары, которые у нее остались». Дети рисуют 6 шаров, зачеркивают 2 из них и показывают движением руки те шары, которые остались у Маши.
Для разъяснения смысла вычитания, так же как и сложения, можно использовать представления детей о соотношении целого и части. В этом случае шары, которые были у Маши («целое»), состоят из двух частей: «шары, которые она подарила» и «шары, которые у нее остались».
Часть всегда меньше целого, поэтому нахождение части связано с вычитанием. Обозначая целое и части их числовыми значениями, дети получают выражение (6-2) или равенство (6-2=4).
б) уменьшение множества, равночисленного данному, на несколько предметов (у детей формируются представления о понятии «меньше на...» («уменьшить на...»), которые связаны с построением совокупности, равночисленной данной («взять столько же»), и ее уменьшением на несколько предметов («без»)). В этом случае совокупность, обозначаемая термином «без», включается в совокупность, обозначаемую термином «столько же». Совокупность, полученная в результате вычитания, является дополнением совокупности, обозначаемой термином «без», до совокупности предметов, обозначаемой термином «столько же».
в) сравнение двух предметных множеств, т. е. ответ на вопрос: «На сколько предметов в одном множестве больше (меньше), чем в другом?»
В процессе выполнения предметных действий у младших школьников формируется представление о вычитании как о действии, которое связано с уменьшением количества предметов.
При рассмотрении ситуации в) в практике обучения обычно учащимся предлагается иллюстрация, по которой проводится следующая беседа:
Учитель задает вопрос: " ""
— В каком ряду кругов больше? (Вопрос почти никогда не вызывает затруднений.)
— На сколько в верхнем ряду предметов больше, чем в нижнем? (Вопрос также не вызывает затруднений, потому что дети ориентируются на количество предметов, оставшихся без пары.) Однако свой ответ первоклассники никак не связывают с выполнением вычитания, так как никаких действий с предметами они не выполняют. Для того чтобы ребята могли осознать связь вопроса: «На сколько больше (меньше)?» с вычитанием, нужно направить их деятельность на решение этой задачи.
8. Методика ознакомления учащихся начальных классов с геометрическими понятиями: точка, отрезок. Построение умозаключения, с помощью которого младшие школьники "открывают" свойство прямоугольника: "В любом прямоугольнике диагонали равны".
Основой формирования представлений о геометрических фигурах является способность детей к восприятию формы. Она позволяет ребенку узнавать, различать и изображать различные геометрические фигуры: точку, прямую, кривую, ломаную, отрезок, угол, многоугольник, квадрат, прямоугольник и т. д. Для этого достаточно показать ему ту или иную геометрическую фигуру и назвать ее соответствующим термином.
Такое знакомство учащихся с геометрическими фигурами позволяет им воспринимать их как целостный образ. Поэтому, если изменить расположение или размер тех фигур, которые были предложены в образце, дети могут допускать ошибки.
Элементарная геометрическая фигура — точка (определение не даётся, только показывается). Любую другую геометрическую фигуру можно рассматривать как множество точек. Через точку можно провести различные линии. Опираясь на свой жизненный опыт, ребенок самостоятельно справляется с задачей проведения линий через точку и даже сам может их назвать соответствующими терминами: «кривая», «прямая» линии.
Примеры заданий:
- прямые линии целесообразно не только изображать на листе бумаги. Используя в качестве модели плоскости тот же лист, получить, например, прямую линию, сгибая его так, чтобы линия сгиба проходила через данную точку.
- аналогично следует действовать и проводя прямую линию через две точки. Дети могут самостоятельно справиться с решением задачи, перегибая лист бумаги так, чтобы линия сгиба проходила через указанные точки. Это позволит им практически убедиться в том, что через две точки можно провести только одну прямую.
- для проведения прямых линий необходимо пользоваться линейкой. Если расположить на доске две точки на большом расстоянии друг от друга и предложить ребятам провести через эти точки прямую линию, то вряд ли кто-либо из них сможет это сделать, не воспользовавшись линейкой.
Полезно, чтобы в процессе выполнения различных упражнений дети научились различать такие понятия, как: «точка пересечения двух линий», «линия проходит через точку», «линия соединяет две точки», «точка принадлежит линии».
При знакомстве с отрезком следует выделить такие его признаки, ориентируясь на которые школьники могли бы легко узнавать эту геометрическую фигуру. Для этого, прежде всего нужно обратить их внимание на то, что отрезок имеет два конца и его (отрезок) следует проводить по линейке.
Если учеников познакомить с отрезком после введения понятия «длина», то помимо названных признаков данного понятия стоит отметить, что у любого отрезка можно измерить длину. Дети могут самостоятельно прийти к выводу, что те прямые линии, которые ими выделены на различных фигурах, по сути дела являются отрезками, так как в них фиксируются два конца. Ориентируясь на рассмотренные признаки отрезков, учащиеся находят их на различных геометрических фигурах: плоскостных и объемных.
Надо также обратить внимание класса на условность изображения прямой и отрезка. А именно: изображая отрезок, мы обязательно фиксируем две точки - концы отрезка, при изображении прямой линии эти точки не фиксируются.
Построение умозаключения, с помощью которого младшие школьники "открывают" свойство прямоугольника: "В любом прямоугольнике диагонали равны".
Прямоугольник – это параллелограмм, у которого все углы прямые».
У параллелограмма противолежащие стороны равны и диагонали точкой пересечения делятся пополам, диагонали параллелограмма равны.
А, значит, в любом прямоугольнике диагонали тоже равны.
9. Методика ознакомления учащихся начальных классов с понятием величины «Длина». Примеры заданий из начального курса математики, раскрывающих смысл разности натуральных чисел – мер величин.
В курсе математики начальных классов дети знакомятся с различными величинами: длина, масса, объем, время, площадь.
При знакомстве с понятием «длина» детям предлагаются различные картинки, а ученики рассказывают, что на них нарисовано, используя слова: длиннее — короче, шире — уже, выше — ниже, ближе — дальше.
Длина отрезка - некоторая положительная величина, определенная для каждого отрезка так, что:
а) равные отрезки имеют равные длины;
б) если отрезок состоит из конечного числа отрезков, то его длина равна сумме их длин.
В математике доказано, что при выбранной единице измерения длина любого отрезка выражается действительным числом и для каждого положительного числа есть отрезок, длина которого выражается этим числом. Основная единица длины — метр. Из этой единицы образуются другие единицы длины: сантиметр, дециметр, миллиметр, километр.
Имеющийся у первоклассников жизненный опыт позволяет им выполнить задание, а затем с помощью учителя перевести свой ответ на язык математики. В данном случае: «длина больше...», «длина меньше...», «длина одинаковая». Большую роль играют ситуации проблемного характера.
Например, на доске прикреплены две полоски (90 см и 120 см). Учитель обращается к классу с вопросом: «Как вы думаете, длина какой полоски больше?» Ученики могут высказать правильное предположение, но его нужно обосновать. Сначала они предлагают известный им способ действия (наложить полоски одну на другую). Но учитель ставит условие: полоски передвигать нельзя. Отыскивая новый способ действия, учащиеся предлагают использовать для этой цели карандаши, ручки, веревочки. Учитель, в свою очередь, предлагает им воспользоваться для обоснования ответа планками различных цветов и размеров: красная — 30 см; синяя — 15 см. Укладывая красную планку по длине первой полоски, дети, пока еще не осознавая этого, проводят измерение. В результате измерения первой полоски они получают число 4, а второй — 3 и самостоятельно приходят к выводу, что 4>3 и, значит, длина первой полоски больше длины второй.
Для сравнения длин полосок необходимо пользоваться одной меркой и числовое значение величины зависит от выбранной единицы. Этот вывод усваивается в процессе выполнения различных учебных заданий.
Для сравнения длин отрезков различными мерками целесообразно познакомить учащихся с циркулем. С помощью этого инструмента дети могут выполнять задания: проводят луч и циркулем откладывают на нем данные отрезки.
С единицей длины — метром — учащихся целесообразно познакомить после того как они научатся читать и записывать трехзначные числа: тогда они смогут пользоваться соотношениями: 1 м=10дм и 1 м=100см для выполнения различных упражнений. С единицей длины — километром — лучше начать действия в теме «Четырехзначные числа», так как только в этом случае учащиеся могут для выполнения различных упражнений пользоваться отношением: 1 км=1000м.
Единица длины — миллиметр — будет востребована после того как дети научатся читать и записывать шестизначные числа. В этом случае они смогут выразить в миллиметрах не только, например, 40 см (40 см=400 мм), но и 40 м (40 м=40000 мм).
10. Методика ознакомления учащихся начальных классов с делением с остатком. Примеры заданий из начального курса математики в случае, когда: а) делимое больше делителя; б) делимое меньше делителя.
Из курса математики вам известно, что «разделить с остатком целое неотрицательное число а на натуральное число b — это значит найти такие целые неотрицательные числа q и r, чтобы a=bq+r и 0 < r< b.
1 -и этап. Постановка учебной задачи. Разъяснение предметного смысла деления с остатком. Знакомство с новой формой записи и с новыми терминами.
Для постановки учебной задачи учитель опирается на знания детей о смысле действия деления и предлагает им объяснить, что обозначают записи, выполненные под каждым рисунком:
• Объясни, что обозначают записи под каждым рисунком:
••• | ••• | ••• | •••
12:3=4 12:4=3
••• | ••• | ••• | ••• | •
13:3=4 (ост.1) 13:4=3 (ост.1)
••• | ••• | ••• | ••• | ••
14:3=4 (ост.2) 14:4=3 (ост.2)
Дети самостоятельно комментируют записи, данные под верхним рисунком, используя знания о смысле деления. Рассматривая второй рисунок и пользуясь известным способом действия, они называют количество кругов в каждой части (3, 3, 3, 3) и обычно заканчивают свой ответ так: «А один круг остался». Поэтому комментирование записей, данных под этим рисунком, также не вызывает у них затруднений (первая запись означает, что 13 кругов делили на части по 3 круга в каждой, получили 4 равных части и один круг остался; вторая запись означает, что 13 кругов разделили на 4 равные части, получили в каждой части по 3 круга и один круг остался. Аналогично комментируются записи под третьим рисунком.
Для подведения учащихся к выводу о том, что остаток при делении должен быть меньше делителя, полезно обсудить следующие вопросы: а) Можно ли к первому рисунку выполнить такую запись: 12:3=3(ост. 3)? (Нет, так как имеем 4 равные части, в каждой из которых по 3 круга); б) Можно ли ко второму рисунку сделать такую запись: 13:3=3 (ост.4)?
Различные упражнения с предметными моделями позволяют либо ученикам высказать предположение о том, что остаток должен быть меньше делителя, либо сам учитель сообщает об этом, а дети проверяют справедливость данного утверждения на различных моделях.
2-й этап. Усвоение смысла деления с остатком. Взаимосвязь различных форм записи деления с остатком.
Средством организации деятельности учащихся на этом этапе являются учебные задания на
• выполнение рисунка по данной записи (лучше, если в этом случае учитель будет использовать как деление без остатка, так и деление с остатком);
• выполнение записи по данным рисункам;
• выбор рисунков, соответствующих данной записи;
• выбор записи, соответствующей данному рисунку.
В процессе выполнения таких заданий учащиеся осознают взаимосвязь между делимым, делителем, неполным частным и остатком.
3-й этап. Овладение способами деления с остатком.
Возможны два способа деления с остатком. Один можно условно назвать подбором делимого, другой способ — подбором неполного частного.
Используя способ подбора делимого, учащиеся рассуждают: «28:5. Делимое 28 не делится на 5. Самое большое число до 28, которое делится на 5, это 25. Разделим 25 на 5, получится 5. Вычтем из 28 число 25, получится остаток 3.
28:5=5 (ост.З)
Остаток 3 меньше, чем делитель 5».
Успешное проведение таких рассуждений во многом зависит от сформированности табличных навыков деления, так как начать свой ответ с фразы «28 не делится на 5» ученик сможет, если быстро вспомнит нужный случай из таблицы деления, что и является показателем прочных и автоматизированных вычислительных навыков.
Но следует заметить, что ориентировка на данный способ действия при делении с остатком не нацеливает детей на осознание той взаимосвязи, которая существует между делимым, делителем, неполным частным и остатком. В результате многие не понимают, что для нахождения остатка нужно из делимого вычесть произведение неполного частного и делителя, а для того, чтобы найти делимое, нужно неполное частное умножить на делитель и прибавить остаток.
Для усвоения этих взаимосвязей более эффективным является выполнение деления способом подбора частного. Ориентировка на него предполагает четкое знание таблицы умножения, что более доступно большинству учащихся. Подбор частного требует применения операций, способствующих осознанию математического смысла деления с остатком.
Например, при делении 57:6 ученик может начать свои действия с подбора частного. Он вспоминает таблицу умножения на 6: 6-8=48, 57-48=9, 9>6; так как остаток не может быть больше делителя, то число 8 не подходит.
Проверим число 9: 6-9=54, 57-54=3, 3<6. Остаток меньше делителя, следовательно, 57:6=9 (ост. 3).
Целесообразно познакомить учащихся с обоими способами деления с остатком. Однако, в качестве приоритетного следует все-таки ориентироваться на способ подбора частного, так как он позволяет детям осознать взаимосвязь делимого, делителя, неполного частного и остатка и использовать эти знания при выполнении различных заданий:
Усвоение учащимися способа подбора частного позволяет им самостоятельно выполнить деление трехзначного числа на двузначное, четырехзначного числа на трехзначное, пятизначного на четырехзначное (при условии получения в частном однозначного числа) до знакомства их с алгоритмом письменного деления.
Используя запись деления «уголком», учащиеся могут выполнить деление четырехзначных чисел на трехзначные.
4-й этап. Деление с остатком меньшего числа на большее.
Для обобщения способов деления с остатком целесообразно рассмотреть случаи деления меньшего числа на большее. Например 7:15. Пользуясь способом подбора делимого, ученики рассуждают: «Найдем число, которое было бы меньше семи и без остатка делилось на 15. Это число нуль. 0:15=0. Теперь найдем остаток: 7-0=7. Получаем 7:15=0(ост.7); 7 меньше 15.
5-й этап. На этом этапе следует рассмотреть случаи деления с остатком на 10, на 100, на 1000 (65:10, 365:100, 5365:1000). Пользуясь различными способами деления с остатком (подбор делимого и подбор частного), а также, выделяя в делимом количество десятков, сотен или тысяч, дети получают неполное частное и остаток. В первом случае остаток 5, во втором случае — 65, в третьем случае — 365.
Методика ознакомления учащихся начальных классов с правилом вычитания числа из суммы. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл умножения натуральных чисел.
Действие вычитания проверяется действием сложения. Число, из которого вычитаем, называется уменьшаемым, а число, которое вычитаем, — вычитаемым. Результат действия вычитания — это разность.
Правило. Чтобы вычесть число из суммы, можно вычесть его из одного из слагаемых и к результату прибавить второе слагаемое.
Правило можно использовать при вычислении натуральных чисел только в случае, если одно из слагаемых больше вычитаемого числа.
Пусть a,b и с - натуральные числа
если a>c, то (a+b)-c=(a-c)+b
если b>c, то (a+b)-c=(b-c)+a
если a>c и b>c, то можно использовать любую из этих формул. (a+b)-c=(a-c)+b=(b-c)+a
1 из случаев вычитания числа из суммы:
(10+4)-6
От десятка уменьшаемого отнимается вычитаемое, которое всегда меньше 10, образуя промежуточное число, которое складываем с оставшейся частью уменьшаемого для получения окончательного ответа.
12. Методика ознакомления учащихся начальных классов с геометрическими понятиями: четырехугольник, прямоугольник. Примеры явных и неявных определений понятий, изучаемых в начальном курсе математики.
Имея представление о точке, отрезке и угле, школьники могут находить эти геометрические фигуры в треугольниках, четырехугольниках, прямоугольниках и квадратах, выделяя в качестве их элементов вершины (точки), стороны (отрезки) и углы. Ориентируясь на эти элементы, дети сумеют распознавать треугольники, четырехугольники, пятиугольники и т. д., называя все эти фигуры многоугольниками.
Примеры заданий:
- учитель предлагает детям рассмотреть различные фигуры. Сначала следует выяснить, как можно их назвать (многоугольники). Затем предлагает учащимся показать и назвать многоугольники, у которых три угла и три стороны; четыре угла и четыре стороны; пять углов и пять сторон и т. д. После этого педагог просит оставить на доске только четырехугольники и выделить из них те, у которых один, два, три, четыре прямых угла (после нескольких попыток некоторые ученики догадаются, что четырехугольников с тремя прямыми углами вообще быть не может). Дети выполняют задание учителя, сначала прикидывая «на глаз», какие углы могут быть прямыми, затем проверяют свое предположение с помощью модели прямого угла.
В результате выделяются четырехугольники, у которых все углы прямые. Они имеют название — прямоугольники. Среди прямоугольников можно выделить такие, у которых все стороны равны. Это квадраты.
Определенную трудность для младших школьников представляет осознание того, что любой квадрат является прямоугольником. Причина в том, что целостный образ квадрата и прямоугольника уже сложился у большинства детей, а умением выделять существенные признаки фигуры они еще не овладели. Поэтому очень важно продумать последовательность вопросов, направленных на выделение существенных признаков прямоугольника и квадрата.
Чтобы показать отношения между понятиями «многоугольник», «четырёхугольник», «прямоугольник» и «квадрат» можно показать схематически.
Примеры заданий:
Пустую схему можно затем использовать для проведения различных игр, например игры «Где мое место?».
Возможна и такая игра: «Кто больше придумает имен». На доске помещается фигура. Дети дают ей названия: многоугольник, четырехугольник, трапеция. Затем помещается другая фигура. Ее можно назвать: многоугольник, четырехугольник, прямоугольник, квадрат. Третью фигуру, изображенную на рисунке, можно назвать: многоугольник, четырехугольник, параллелограмм, ромб.
13. Методика ознакомления учащихся начальных классов с правилом умножения числа на сумму. Примеры заданий из начального курса математики, раскрывающих смысл произведения натуральных чисел – мер величин.
Распределительное свойство умножения также целесообразно объяснять на основе приема соотнесения предметных и символических моделей, который создает условия для анализа, сравнения, обобщения и понимания детьми формулировки данного свойства. Предлагаются задания:
Догадайся: что обозначают выражения, записанные под каждым рисунком? Чем они похожи? Чем отличаются? Вычисли их значения.






 а)
а)
 |  |  |  |  |  |  | |||||||
 |  |  |  |  |  |  |
3*5+3*2
3*(5+2)
Сколько всего квадратов в красном и синем прямоугольниках?
 |
Маша ответила на вопрос так:
4*6+4*3=36 (кв.).
Миша — так:
4*(6+3)=36 (кв.).
Как рассуждали Маша и Миша? Кто из них прав?
Главным средством усвоения распределительного свойства умножения также являются учебные задания. Например:
Вставь знаки <, > или =, чтобы получились верные записи:
3*(14+8) 3*14+3*8
6*(27+8) 6*27+8
18*(36+4) 40*18
Вставь пропущенные числа, чтобы равенства были верными:
а) 3*(8+)= +3*4
б) 5*(+)=35+45
Знакомство школьников с распределительным свойством умножения позволяет им самостоятельно «открыть» рациональный вычислительный прием устного умножения двузначного числа на однозначное, проверять результаты вычислений, используя различные способы, а также находить различные методы решения текстовых задач.
Методика ознакомления учащихся начальных классов с алгоритмом письменного сложения. Примеры заданий из учебников математики для начальной школы, раскрывающих теоретические основы алгоритма сложения многозначных чисел в десятичной системе счисления.
Алгоритм сложения:
1. Записывают второе слагаемое под первым так, чтобы соответствующие разряды находились друг под другом.
2. Складывают цифры разряда единиц. Если сумма меньше 10, ее записывают в разряд единиц ответа и переходят к следующему разряду.
3. Если сумма цифр единиц больше или равна 10, то представляют ее в виде: 10+С0, где С0 — однозначное число; записывают С0 в разряд единиц ответа и прибавляют 1 к цифре десятков первого слагаемого, после чего переходят к разряду десятков.
4. Повторяют те же действия с десятками, потом с сотнями и т. д. Процесс сложения заканчивается, когда произведено сложение цифр старших разрядов.
Безусловно, младшие школьники не могут усвоить алгоритмы письменного сложения в общем виде. Но учителю знать их необходимо. Это позволит ему:
а) при ознакомлении учащихся с алгоритмом правильно организовать подготовительную работу;
б) управлять деятельностью школьников, направленной на усвоение алгоритма;
в) подбирать и составлять различные задания, нацеленные на усвоение операций, входящих в алгоритмы письменного сложения.
Приведенный выше алгоритм даётся учащимся начальных классов в упрощенном виде, где фиксируются только основные моменты:
• Второе слагаемое нужно записать под первым так, чтобы соответствующие разряды находились друг под другом;
• Сложение следует начинать с низшего разряда, т. е. складывать сначала единицы.
Для формирования общего способа действий целесообразно познакомить учащихся с алгоритмами письменного сложения после того, как они усвоят нумерацию чисел в пределах миллиона. При этом их деятельность должна быть направлена не на отработку частных случаев сложения, а на осознание тех операций, которые входят в алгоритмы. Для этого уже при изучении нумерации полезно обратить внимание детей на то, как изменяется цифра, стоящая в определенном разряде данного числа при его увеличении на разрядные единицы, десятки, сотни, тысячи
В процессе этих упражнений дети осознают соотношение разрядов и значение каждой цифры в записи числа. Это способствует сознательному усвоению механизма письменного сложения.
Приступая к изучению алгоритмов письменного сложения, учащимся полезно предложить задания:
На сколько можно увеличить число 308287, чтобы изменились цифры, стоящие в разряде единиц и десятков, а цифры в других разрядах остались те же?
Сколько однозначных чисел можно прибавить к числу 235438, чтобы изменились только цифры, стоящие в разряде единиц и десятков?
В результате обсуждения этих заданий дети самостоятельно делают вывод: если получаем в соответствующем разряде 10 единиц или больше 10 единиц, „то изменяется цифра следующего высшего разряда
Цифры, обозначающие число десятков, сотен, тысяч и т. д., переносимые в высший разряд, можно фиксировать в записи сложения над соответствующим разрядом:
Запиши пять чисел, в которых 80 тысяч. Увеличь каждое на 8739. Вычисли значения сумм «в столбик».
Методика ознакомления учащихся начальных классов с действием умножения. Примеры заданий из учебников математики для начальной школы, раскрывающих теоретические основы алгоритма умножения многозначных чисел в десятичной системе счисления.
Из курса математики вам известно, что если а и b целые неотрицательные числа, то:
а) а • b = a+a+a+...+а, при b> 1;
б) а- 1= a, при b =1;
в)а-0=0, при b =0.
В основе разъяснения младшим школьникам смысла умножения лежит теоретико-множественная трактовка этого определения. Она легко переводится на язык предметных действий и позволяет при усвоении нового понятия активно использовать ранее изученный материал. Для осознания необходимости введения нового действия можно полезно придумать (подготовить) реальные ситуации. Например: требуется посчитать количество кафельных плиток для выкладки стены на кухне. Стена имеет форму прямоугольника, разбитого на квадраты. Посчитав квадраты в одном ряду и убедившись в том, что их количество во всех рядах одинаково, ученики записывают сумму одних и тех же слагаемых.
Учитель сообщает, что сложение одинаковых слагаемых в математике называют умножением. И показывает запись, которую используют в математике для сложения одинаковых слагаемых. Например: 9+9+9+9+9=9*5; 7+7+7+7+7+7=7*6. — Кто догадается, что обозначают в записях справа первое и второе число? Ответ на вопрос требует использования приемов анализа и синтеза, сравнения и обобщения. (Первое число показывает — какие слагаемые складывают, второе число — сколько таких слагаемых).
Примеры зданий (ИСТОМИНА 2 класс!!!)
При изучении данной темы необходимо рассмотреть случаи умножения на нуль и на единицу. Для этой цели можно воспользоваться таким заданием:
Вычисли значения произведений, заменив умножение сложением. Догадайся, почему некоторые выражения записаны в рамках:
8*2 5*3 12*1
7*4 6*1 13*4
8*1 9-3 15*0
Важно, чтобы при выполнении данного задания все дети поняли, что умножение на 0 и на 1 мы не можем заменить сложением. Эти случаи нужно запомнить, так как математики договорились, что при умножении любого числа на 1 мы получаем это же число. При умножении любого числа на нуль, мы получаем нуль.
Понятие «увеличить в...» целесообразно ввести сразу после знакомства со смыслом умножения, предложив задание, с которым учащиеся смогут справиться самостоятельно.
Одновременное использование в одном задании понятий «увеличить на...» и «увеличить в...» позволит ученикам лучше дифференцировать их и допускать меньше ошибок, применяя эти понятия к решению различных задач.
ЗАДАНИЯ НА СООТНЕСЕНИЕ РИСУНКА И ЗАПИСЕЙ – ИСТОМИНА 2 класс!!!!
Дата добавления: 2015-02-16; просмотров: 727 | Поможем написать вашу работу | Нарушение авторских прав |