
Читайте также:
|
Пусть имеется функция  , от которой мы вычислили первую производную
, от которой мы вычислили первую производную  . Но
. Но  снова является функцией и от нее можно тоже вычислить производную. Производная от первой производной т.е.
снова является функцией и от нее можно тоже вычислить производную. Производная от первой производной т.е.  называется второй производной и обозначается
называется второй производной и обозначается  :
:
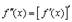
Аналогично, производная от второй производной называется третьей производной
 .
.
Аналогично определяются производные более высоких порядков. Отметим только, что производные более высоких порядков отмечаются не штрихами (их было бы слишком много) а цифрами, заключенными в скобки -  ,
,  и т.д.
и т.д.
Итак, производная n-го порядка определяется как производная от производной (n-1)-го порядка

Основные формулы, касающиеся производных высших порядков, следующие:
1. 
2. 
3. 
Ппроизводной нулевого порядка считается сама функция, т.е.  .
.
Аналогично этому, дифференциалом второго порядка называется дифференциал от первого дифференциала, т.е.

Выведем формулу для  . Имеем
. Имеем

При дальнейшем преобразовании следует иметь в виду, что  , совпадающее с приращением аргумента
, совпадающее с приращением аргумента  , есть величина, совершенно не зависимая от
, есть величина, совершенно не зависимая от 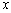 , т.к. мы
, т.к. мы 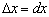 можем взять каким угодно. Поэтому по отношению к
можем взять каким угодно. Поэтому по отношению к 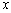

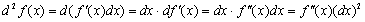 .
.
Скобки у  обычно не пишут
обычно не пишут

Отсюда
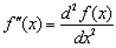
Аналогично, дифференциал третьего порядка определяется как дифференциал от второго дифференциала

Имеем


так что
 ;
; 
В общем случае

Легко показывается по индукции, что
 ;
; 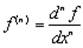 .
.
Дата добавления: 2015-01-30; просмотров: 126 | Поможем написать вашу работу | Нарушение авторских прав |