Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Асимметрия, эксцесс. Вычисление

Вычисление асимметрии и эксцесса позволяет установить симметричность распределения случайной величины относительно Для этого находят третий центральный момент, характеризующий асимметрию закона распределения случайной величины. Если он равен нулю 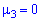, то случайная величина симметрично распределена относительно математического ожидания Поскольку 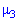имеет размерность случайной величины в кубе, то вводят безразмерную величину — коэффициент асимметрии:

Центральный момент четвертого порядка используется для определения эксцесса, характеризует плосковершиннисть или гостровершиннисть плотности вероятности Эксцесс вычисляется по формуле

Число 3 вычитается для сравнения отклонения от центрального закона распределения (нормального закона), для которого подтверждается равенство:

Итак, 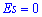для нормального закона распределения. Если эксцесс положительный то на графике функция распределения остро вершину и для отрицательных значений более пологую. Таким образом можно установить отклонения заданного закона от нормального. Для наглядности при различных значениях асимметрии и эксцесса графики плотности вероятностей изображены на рисунках ниже

51 Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:

где: 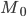— значение моды — нижняя граница модального интервала — величина интервала — частота модального интервала 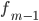— частота интервала, предшествующего модальному — частота интервала, следующего за модальным

Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот , а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:

М_е = (n_{(число признаков в совокупности)} + 1)/2,

в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).

При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:

где: — искомая медиана — нижняя граница интервала, который содержит медиану — величина интервала — сумма частот или число членов ряда - сумма накопленных частот интервалов, предшествующих медианному — частота медианного интервал

40 Функцией распределения вероятностей называют функцию 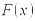, определяющую вероятность того, что случайная величина в результате испытания примет значение, меньшее , то есть:
.
Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

Свойства функции распределения вероятностей случайной величины1. Значения функции распределения вероятностей принадлежат отрезку :
. 2. Функция распределения вероятностей – неубывающая функция, то есть:
, если . Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале , равна приращению функции распределения вероятностей на этом интервале:
.
Следствие 2. Вероятность того, что непрерывная случайная величина примет одно определенное значение, равна нулю.
Используя последнее следствие, легко убедиться в справедливости следующих равенств:
. 3. Если возможные значения непрерывной случайной величины принадлежат интервалу , то:
, если ;
, если . Следствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения:
; .