Читайте также:
|
Берілген интегралды интегралдау әдістері интеграл астындағы функцияның берілуіне және интегралдар кестесінің қорына байланысты бірнеше түрге бөлінеді:1)тікелей интегралдау; 2)айнымалыларды ауыстыру арқылы интегралдау;
3) бөліктеп интегралдау. ОСы тәсілдердің әрқайсысына жеке-жеке тоқталайық.
1.Тікелей интегралдау. Көптеген функцияларды анықталмаған интегралдың қасиеттері мен интегралдау кестесіне сүйеніп тікелей интегралдауға болады. Тікелей интегралдау тәсіліне бірнеше мысалдар келтірейік.
Мысалы -1.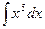 
интегралын есептеу керек.
Шешуі. 
болған жағдайда III формуланы қолданамыз:
Мысал-2. 
интегралын табу керек.
Шешуі. 
. Тұрақты 3-ті интеграл белгісінің алдына шығарып, сонан кейін III формуланы n=-3 болған жағдай үшін қолдансақ, мынау шығады:
Мысал-3. 
интегралын табу керек.
Шешуі. Екі мүшелікті үшінші дәрежеге шығарамыз да, әрбір қосылғышты дәреже түрінде жазамыз, сонан кейін 
және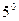 
қасиеттерді пайдалана отырып, III формуланы қолдансақ, мынау шығады:
ЕСКЕРТПЕ. Әрбір қосылғыштың соңына ерікті тұрақтыны жазып отырудың қажеті жоқ, өйткені ерікті тұрақтылардың қосындысы да – ерікті тұрақты, ал оны біз ең соңына жаздық.
Мысал-4.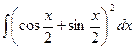 
интегралын есептеу керек.
Шешуі. Екі мүшелікті квадраттап алып, II және VII формулаларын қолдансақ,
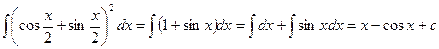болады.
Мысал-5.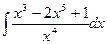 
интегралын есептеу керек.
Шешуі. Интеграл астындағы функцияның алымын мүшелеп бөліміне бөлеміз де, сонан кейін және 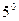қасиеттері мен III, IV формулаларды қолданамыз. Сонда,
болады.
Мысал-6. 
интегралын есептеу керек.
Шешуі. Әуелі интегралды 3-ке көбейтеміз де бөлеміз, сонан кейін алымына 
-ты қосамыз да аламыз. Сонда нәтиже мынандай болады:
.
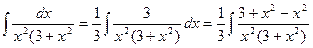Соңғы интегралды екі интегралдың айырымы түріне келтіріп аламыз да, сонан кейін III және XV формулалардың жәрдеміммен интегралдасақ,
болады.
Мысал-7. 
интегралын есептеу керек.
Шешуі. 
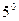болатынын ескеріп, және қасиеттерді және III формуланы қолдансақ, мынандай нәтижеге келеміз:
.
Мысал-8. 
интегралын есептеп шығару керек.
Шешуі. Рационал бөлшек 
-ның бүтін бөлігін бөліп шығарамыз яғни: 
.
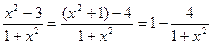қасиет пенIII, XV формулаларды қолдансақ, мынаны табамыз:
.
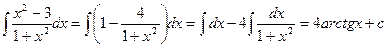Дата добавления: 2015-04-11; просмотров: 149 | Поможем написать вашу работу | Нарушение авторских прав |