
Читайте также:
|
Сезонные колебания (сезонная неравномерность) – это сравнительно устойчивые внутригодичные колебания, когда из года в год в одни месяцы уровень явления повышается, а в другие – снижается. Перед статистикой стоит задача выявить сезонную неравномерность и измерить ее размеры. Существует несколько подходов к анализу структуры временных рядов, содержащих сезонные или циклические колебания. 
Простейший подход – расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда. Общий вид аддитивной модели следующий:

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент. Общий вид мультипликативной модели выглядит так:

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение компонент. Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
Процесс построения модели включает в себя следующие шаги.
1. Выравнивание исходного ряда методом скользящей средней.
2. Расчет значений сезонной компоненты S.
3. Устранение сезонной компоненты из исходных уровней ряда и получение выравненных данных (Т+Е) в аддитивной или (ТЕ) в мультипликативной модели.
4. Аналитическое выравнивание уровней (Т+ Е) или (Т Е) и расчет значений Т с использованием полученного уравнения тренда.
5. Расчет полученных по модели значений (Т+ S) или (Т- S).
6. Расчет абсолютных и/или относительных ошибок.
Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок E для анализа взаимосвязи исходного ряда и других временных рядов.
Пример. Построение аддитивной модели временного ряда. Из данных об объеме потребления электроэнергии жителями района за последние четыре года следует, что временной ряд содержит сезонные колебания периодичностью, так как в осенне-зимний период времени (I и IVкварталы) выше, чем весной и летом (II и III кварталы). По графику этого ряда (рис. 2) можно установить наличие приблизительно равной амплитуды колебаний. Это свидетельствует о возможном существовании в ряде аддитивной модели.
Таблица 1
Расчет оценок сезонной компоненты в аддитивной модели
| № квартала, t | Потребление электроэнергии,

| Итого за четыре квартала | Скользящая средняя за четыре квартала | Центрированная скользящая средняя | Оценка сезонной компоненты | ||
| 6,0 | - | - | |||||
| 4,4 | - | - | - | - | |||
| 5,0 | 24,4 | 6,10 | 6,250 | -1,250 | |||
| 9,0 | 25,6 | 6,40 | 6,450 | 2,550 | |||
| 7,2 | 26,0 | 6,50 | 6,625 | 0,575 | |||
| 4,8 | 27,0 | 6,75 | 6,875 | -2,075 | |||
| 6,0 | 28,0 | 7,00 | 7,100 | -1,100 | |||
| 10,0 | 28,8 | 7,20 | 7,300 | 2,700 | |||
| 8,0 | 29,6 | 7,40 | 7,450 | 0,550 | |||
| 5,6 | 30,0 | 7,50 | 7,625 | -2,025 | |||
| 6,4 | 31,0 | 7,75 | 7,875 | -1,475 | |||
| 11,0 | 32,0 | 8,00 | 2,875 | ||||
| 9,0 | 33,0 | 8,25 | 8,325 | 0,675 | |||
| 6,6 | 33,6 | 8,40 | 8,375 | -1,775 | |||
| 7,0 | 33.4 | 8,35 | |||||
| 10,8 | |||||||

Рис. 2. Потребление электроэнергии жителями региона
1. Проводится выравнивание исходных уровней ряда методом скользящей средней. Для этого суммируются уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определяются условные годовые объемы потребления электроэнергии (гр 3). Далее разделив полученные суммы на 4, определяются скользящие средние (гр 4). Полученные выравненные значения уже не содержат сезонной компоненты. Эти значения приводятся в соответствие с фактическими моментами времени, для чего рассчитываются средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5).
2. Оценки сезонной компоненты определяются как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6). Эти оценки для расчета значений сезонной компоненты S в аддитивной модели (табл. 2). В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Таблица 2
Расчет значений сезонной компоненты в аддитивной модели
| Показатели | Год | № квартала | |||
| I | II | III | IV | ||
| - 0,575 0,550 0,675 | - -2,075 -2,025 -1,775 | -1,250 -1,100 -1,475 - | 2,550 2,700 2,875 - | ||
| Итого за i-й квартал (за все годы) | 1,800 | -5,875 | -3,825 | 8,125 | |
Средняя оценка сезонной компоненты для i-го квартала, 
| 0,600 | -1,958 | -1,275 | 2,708 | |
Скорректированная сезонная компонента, 
| 0,581 | -1,977 | -1,294 | 2,690 |
Для данной модели:
0,6 – 1,958 – 1,275 + 2,708 = 0,075.
Определим корректирующий коэффициент:
k = 0,075/4 = 0,01875.
Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом k:
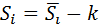 , где i =1,…,4
, где i =1,…,4
.
Проверим условие равенства нулю суммы значений сезонной компоненты:
0,581 – 1,977 – 1,294 + 2,690 = 0.
Таким образом, получены следующие значения сезонной
компоненты:
I квартал: S1=0,581;
II квартал: S2 = - 1,979;
III квартал: S3 = -1,294;
IV квартал: S4= 2,690.
Влияние сезонной компоненты элиминируется, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины Т + Е = Y- S (гр. 4 табл.3). Эти значения рассчитываются за каждый момент времени и содержат тенденцию и случайную компоненту:
Таблица 3
| t | 
| 
| 
| 
| 
| 
| 
|
| 6,0 | 0,581 | 5,419 | 5,901 | 6,482 | -0,482 | 0,232 | |
| 4,4 | -1,977 | 6,377 | 6,087 | 4,110 | 0,290 | 0,084 | |
| 5,0 | -1,294 | 6,294 | 6,273 | 4,979 | 0,021 | 0,000 | |
| 9,0 | 2,690 | 6,310 | 6,459 | 9,149 | -0,149 | 0,022 | |
| 7,2 | 0,581 | 6,619 | 6,645 | 7,226 | -0,026 | 0,001 | |
| 4,8 | -1,977 | 6,777 | 6,831 | 4,854 | -0,054 | 0,003 | |
| 6,0 | -1,294 | 7,294 | 7,017 | 5,723 | 0,277 | 0,077 | |
| 10,0 | 2,690 | 7,310 | 7,203 | 9,893 | 0,107 | 0,011 | |
| 8,0 | 0,581 | 7,419 | 7,389 | 7,970 | 0,030 | 0,001 | |
| 5,6 | -1,977 | 7,577 | 7,575 | 5,598 | 0,002 | 0,000 | |
| 6,4 | -1,294 | 7,694 | 7,761 | 6,467 | -0,067 | 0,004 | |
| 11,0 | 2,690 | 8,310 | 7,947 | 10,637 | 0,363 | 0,132 | |
| 9,0 | 0,581 | 8,419 | 8,133 | 8,714 | 0,286 | 0,082 | |
| 6,6 | -1,977 | 8,577 | 8,319 | 6,342 | 0,258 | 0,067 | |
| 7,0 | -1,294 | 8,294 | 8,505 | 7,211 | -0,211 | 0,045 | |
| 10,8 | 2,690 | 8,110 | 8,691 | 11,381 | -0,581 | 0,338 |
4. Определяется компоненту  данной модели с помощью аналитическое выравнивание ряда (Т+Е) с использованием линейного тренда:
данной модели с помощью аналитическое выравнивание ряда (Т+Е) с использованием линейного тренда:

Линейный тренд описывается следующей формулой:
Т= 5,715 + 0,186 t
Подставляя в это уравнение значения t =1,...,16, находятся уровни Т для каждого момента времени (гр. 5).График уравнения тренда приведен на рис. 3.

Рис. 3. Потребление электроэнергии жителями района (фактические, выравненные и полученные по аддитивной модели значения уровней ряда)
5. Для нахождения значения уровней ряда, полученных по аддитивной модели к уровням T прибавляется значения сезонной компоненты для соответствующих кварталов.
6. В соответствии с методикой построения аддитивной модели расчет ошибки производится по формуле:

Это абсолютная ошибка (гр.7 табл 3).
По аналогии с моделью регрессии для оценки качества пост-
роения модели или для выбора наилучшей модели можно применять сумму квадратов полученных абсолютных ошибок. Для данной аддитивной модели сумма квадратов абсолютных ошибок равна 1,10. По отношению к общей сумме квадратов отклонений уровней ряда от его среднего уровня, равной 71,59, эта величина составляет чуть более 1,5%:
(1,10 /67,12) ·100 = 1,63%.
Следовательно, аддитивная модель объясняет 98,4% общей вариации уровней временного ряда потребления электроэнергии за последние 16 кварталов.
Пример. Построение мулътипликативной модели временного ряда. Пусть имеются поквартальные данные о прибыли компании за последние четыре года.
Таблица 4
Прибыль компании, тыс. долл. США
 Квартал
Год Квартал
Год
| I | И | Ш | IV |
График данного временного ряда свидетельствует о наличии сезонных колебаний (период колебаний равен 4) и общей убывающей тенденции уровней ряда:

Рис. 4. Динамика прибыли компании
1. Прибыль компании в весенне-летний период выше, чем в осенне-зимний период. Поскольку амплитуда сезонных колебаний уменьшается, можно предположить существование мультипликативной модели.
Таблица 4
Расчет оценок сезонной компоненты в мультипликативной модели
| № квартала | Прибыль компании,

| Итого за четыре квартала | Скользящая средняя за четыре квартала | Центрированная скользящая средняя | Оценка сезонной компоненты |
| - | - | - | |||
| - | - | - | |||
| 81,5 | 81,25 | 1,108 | |||
| 81,0 | 0,800 | ||||
| 79,0 | 77,75 | 0,900 | |||
| 76,5 | 75,75 | 1,215 | |||
| 75,0 | 1,081 | ||||
| 73,0 | 71,5 | 0,811 | |||
| 70,0 | 68,5 | 0,905 | |||
| 67,0 | 65,75 | 1,217 | |||
| 64,5 | 63,25 | 1,075 | |||
| 62,0 | 59,5 | 0,807 | |||
| 57,0 | 54,75 | 0,950 | |||
| 52,5 | 50,25 | 1,194 | |||
| 48,0 | - | - | |||
| - | - | - | - |
2. Оценки сезонной компоненты находятся как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 4). Эти оценки используются для расчета значений сезонной компоненты S (табл. 5). Для этого находятся средние за каждый квартал оценки сезонной компоненты. Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в
цикле (в примере – число периодов одного цикла (год) равно 4 кварталам.
Таблица 5
Расчет сезонной компоненты в мультипликативной модели
| Показатели | Год | № квартала, i | |||
| I | II | III | IV | ||
| - 0,900 0,905 0,950 | - 1,215 1,217 1,194 | 1,108 1,081 1,075 - | 0,800 0,817 0,807 - | ||
| Итого за i -й квартал (за все годы) | 2,755 | 3,626 | 3,264 | 2,424 | |
Средняя оценка сезонной компоненты для i -го квартала, 
| 0,918 | 1,209 | 1,088 | 0,808 | |
Скорректированная сезонная компонента, 
| 0,913 | 1,202 | 1,082 | 0,803 |
0,918 + 1,209 + 1,088 + 0,808 =4,023.
Определим корректирующий коэффициент:
k = 4/4,023 = 0,9943.
Определим скорректированные значения сезонной компоненты, умножив ее средние оценки на корректирующий коэффициент k:
 , где i =1,…,4
, где i =1,…,4
Проверим условие равенства 4 суммы значений сезонной компоненты:
0,913 + 1,202 + 1,082 + 0,803 = 4.
Получим следующие значения сезонной компоненты:
| I квартал: | S1 =0,913; |
| II квартал: | S2 = 1,202; |
| III квартал | S3 = 1,082; |
| IV квартал: | S4 == 0,803. |
Занесем полученные значения в табл. 6 для соответствующих кварталов каждого года (стр. 3).
Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты, т.е. получим величины  (гр. 4 табл. 6), которые содержат только тенденцию и случайную компоненту.
(гр. 4 табл. 6), которые содержат только тенденцию и случайную компоненту.
Таблица 6
Расчет выравненных значений Т и ошибок Е в мультипликативной модели
| t | 
| 
| 
| T | 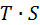
| 
| 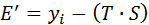
| 
|
| 0,913 | 78,86 | 87,80 | 80,16 | 0,898 | -8,16 | 66,55 | ||
| 1,202 | 83,19 | 85,02 | 102,20 | 0,979 | -2,20 | 4,82 | ||
| 1,082 | 83,18 | 82,25 | 88,99 | 1,011 | 1,01 | 1,02 | ||
| 0,803 | 79,70 | 79,47 | 63,82 | 1,003 | 0,18 | 0,03 | ||
| 0,913 | 76,67 | 76,70 | 70,03 | 1,000 | -0,03 | 0,00 | ||
| 1,202 | 76,54 | 73,93 | 88,86 | 1,035 | 3,14 | 9,87 | ||
| 1,082 | 73,94 | 71,15 | 76,99 | 1,039 | 3,01 | 9,08 | ||
| 0,803 | 72,23 | 68,38 | 54,91 | 1,056 | 3,09 | 9,56 | ||
| 0,913 | 67,91 | 65,60 | 59,90 | 1,035 | 2,10 | 4,42 | ||
| 1,202 | 66,56 | 62,83 | 75,52 | 1,059 | 4,48 | 20,06 | ||
| 1,082 | 62,85 | 60,06 | 64,98 | 1,046 | 3,02 | 9,12 | ||
| 0,803 | 59,78 | 57,28 | 46,00 | 1,044 | 2,00 | 4,01 | ||
| 0,913 | 56,96 | 54,51 | 49,77 | 1,045 | 2,23 | 4,99 | ||
| 1,202 | 49,92 | 51,73 | 62,18 | 0,965 | -2,18 | 4,77 | ||
| 1,082 | 46,21 | 48,96 | 52,97 | 0,944 | -2,97 | 8,85 | ||
| 0,803 | 37,36 | 46,19 | 37,09 | 0,809 | -7,09 | 50,23 |
Для определения компоненты Т в мультипликативной модели рассчитываются параметры линейного тренда, используя уровни ( ):
):

|
Уравнение тренда имеет следующий вид:
Т= 90,57 -2,774 t.
Подставляя в это уравнение значения t = 1, …, 16, находятся уровни Т для каждого момента времени (гр. 5 табл. 6). График уравнения тренда приведен на рис. 5.

Рис 5. Прибыль компании (фактические и выравненные по мультипликативной модели значения уровней ряда)
5. Находятся уровни ряда по мультипликативной модели, умножив уровни Т на значения сезонной компоненты для соответствующих кварталов. Графически значения (T·S) представлены на рис. 5.
6. Расчет ошибки в мультипликативной модели производится по формуле:

Численные значения ошибки приведены в гр. 7 табл. 6. Если временной ряд ошибок не содержит автокорреляции, его можно использовать вместо исходного ряда для изучения его взаимосвязи с другими временными рядами. Для того чтобы сравнить мультипликативную модель и другие модели временного ряда, можно по аналогии с аддитивной моделью использовать сумму квадратов абсолютных ошибок. Абсолютные ошибки в
мультипликативной модели определяются как
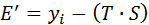
В данной модели сумма квадратов абсолютных ошибок составляет 207,20. Общая сумма квадратов отклонений фактических уровней этого ряда от среднего значения равна 5023, т.е. доля объясненной дисперсии уровней ряда равна:
(1 - 207.38/5023) = 0,959, или 95,9%.
Выявление и устранение сезонного эффекта (в некоторых источниках применяется термин «десезонализация уровней ряда») используются в двух направлениях. Во-первых, воздействие сезонных колебаний следует устранять на этапе предварительной обработки исходных данных при изучении взаимосвязи нескольких временных рядов. Поэтому в российских и международных статистических сборниках часто публикуются данные, в которых устранено влияние сезонной компоненты (если это помесячная
или поквартальная статистика), например показатели объемов производства в отдельных отраслях промышленности, уровня безработицы и т.д. Во-вторых, это анализ структуры одномерных временных рядов с целью прогнозирования уровней ряда в будущие моменты времени.
Дата добавления: 2015-04-12; просмотров: 1107 | Поможем написать вашу работу | Нарушение авторских прав |