Читайте также:
|
Стохастической связью между случайными величинами называется такая связь, при которой с изменением одной величины меняется распределение другой. Функциональной зависимостью называется такая связь между случайными величинами, при которой при известном значении одной из величин можно точно указать значение другой. В отличие от функциональной связи при стохастической связи с изменением величины 
величина 
имеет лишь тенденцию изменяться. По мере увеличения тесноты стохастической зависимости она все более приближается к функциональной, а в пределе ей соответствует.
Крайняя противоположность функциональной связи — полная независимость случайных величин. Если случайные величины независимы, то согласно теореме умножения получаем
Условие 
можно использовать в качестве необходимого и достаточного критерия независимости двух случайных величин, если известны плотности распределения системы и случайных величин, в нее входящих. При неизвестном законе распределения системы для оценки тесноты стохастической связи чаще всего используется коэффициент корреляции. Дисперсия суммы двух случайных величин X и Y равна
Если X и Y независимы, то
Зависимость между X и Y существует, если
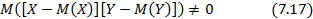
Это величина называется корреляционным моментом, или ковариацией cov{XY}, (covxy) случайных величин. Она характеризует не только зависимость величин, но и их рассеяние. Из (7.17) следует, что если одна из величин мало отклоняется от своего математического ожидания, то ковариация будет мала даже при тесной стохастической связи. Чтобы избежать этого, для характеристики связи используют безразмерную величину, называемую коэффициентом корреляции:
(7.18)
где 
и 
— стандартные отклонения X и Y.
Случайные величины, для которых ковариация (значит, и коэффициент корреляции) равна нулю, называются некоррелированными. Равенство нулю коэффициента корреляции не всегда означает, что случайные величины X и Y независимы: связь может проявляться в моментах более высокого порядка (по сравнению с математическим ожиданием). Только в случае нормального распределения при 
связь между случайными величинами однозначно отсутствует. Плотность нормального распределения системы двух случайных величин выражается следующей формулой:
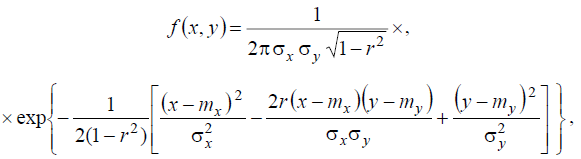(7.19)
где 
— коэффициент корреляции. Если X и Y некоррелированы (т. е. 
), то из (7.19) следует, что
(7.20)
т. е. нормально распределенные случайные величины X и Y не только некоррелированы, но и независимы. Отметим следующие свойства коэффициента корреляции:
1) величина 
не меняется от прибавления к X и Y неслучайных слагаемых;
2) величина не меняется от умножения X и Y на положительные числа;
3) если одну из величин, не меняя другой, умножить на –1, то на –1 умножится и коэффициент корреляции.
Тогда, если от исходных величин перейти к нормированным
величина не изменится: 
Из (7.16) и (7.18) следует, что
Для нормированных величин 
, тогда
Аналогично в случае разности (X – Y) можно получить, что
По определению дисперсии
следовательно
При 
имеем линейные функциональные зависимости вида
при этом если 
, то 
; если 
, то 
.
Если мeжду величинами X и Y имеется произвольная стохастическая связь, то 
. При 
говорят о положительной корреляционной связи между X и Y, при 
— об отрицательной. Следует учитывать, что коэффициент корреляции характеризует не любую зависимость, а только линейную.
Для нормально распределенной системы двух случайных величин можно доказать, что
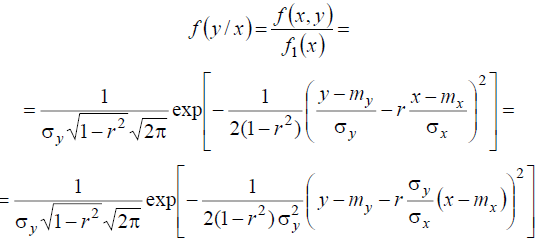(7.25)
Условная плотность распределения величины Y соответствует плотности нормального распределения с математическим ожиданием
(7.26)
и среднеквадратичным отклонением
(7.27)
Величина my/x называется условным математическим ожиданием величины Y при данном Х. Линейная зависимость (7.26) — регрессией Y на X. По аналогии прямая
(7.28)
есть регрессия X на Y.
Линии регрессии совпадают только при наличии линейной функциональной зависимости. Из (7.26) и (7.28) видно, что для независимых X и Y линии регрессии параллельны координатным осям.
Дата добавления: 2015-04-12; просмотров: 269 | Поможем написать вашу работу | Нарушение авторских прав |