Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Системы случайных величин. Функция и плотность распределения системы двух случайных величин. Условные законы распределения

ЛЕКЦИЯ 7

Системы случайных величин. Функция и плотность распределения системы двух случайных величин. Условные законы распределения. Стохастическая связь. Ковариация. Коэффициент корреляции, его свойства. Линии регрессии. Выборочный коэффициент корреляции; проверка гипотезы об отсутствии корреляции. Приближенная регрессия; метод наименьших квадратов.

Системы случайных величин. Функция и плотность распределения системы двух случайных величин. Условные законы распределения

На практике чаще всего приходится иметь дело с экспериментами, результатом которых является не одна случайная величина, а две и более, образующие систему. Свойства системы случайных величин не ограничиваются свойствами величин, в нее входящих; они определяются также взаимосвязью (зависимостями) этих случайных величин. Информация о каждой случайной величине, входящей в систему, содержится в ее законе распределения.

Рассмотрим систему из двух случайных величин Х и Y. Функцией распределения такой системы называется вероятность совместного выполнения двух неравенств

Плотность распределения системы определяется как вторая смешанная производная

(7.2)

Вероятность попадания точки (Х, Y) в произвольную область D равна (7.3)

Свойства плотности распределения:

1) она является неубывающей функцией:

2) вероятность попадания случайной точки на всю координатную плоскость равна вероятности достоверного события:

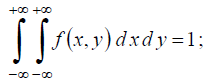(7.5)

3) функция распределения выражается через плотность распределения как

(7.6)

4) плотность распределения каждой из случайных величин можно получить следующим образом:

(7.7)

(7.9)

Чтобы полностью охарактеризовать систему (т. е. получить ее закон распределения), кроме распределения каждой величины, входящей в систему, необходимо знать и связь между этими величинами. Эта зависимость характеризуется с помощью условных законов распределения.

Условным законом распределения величины Y, входящей в систему , называется ее закон распределения при условии, что другая случайная величина Х приняла определенное значение х. Условная функция распределения обозначается плотность распределения — . Для условных плотностей распределений справедлива теорема умножения законов распределения:

Тогда

(7.12)