Читайте также:
|
1. Разложить многочлен P(z)= 
на линейные множители.
2.Решить уравнение. Ответ представить в алгебраической форме и изобразить на комплексной плоскости.
3. Установить, являются ли заданные множества подпространствами в R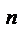 
. В случае положительного ответа найти базис и размерность подпространства.
1) Множество векторов, координаты которых удовлетворяют условию: 
2) Множество векторов, координаты которых удовлетворяют условию: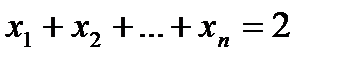 
3) Множество векторов, координаты которых (
- отрицательные числа.
4. Пусть L-множество многочленов p(t) степени не выше 2, удовлетворяющих условию:
p(0)=p(1). Доказать, что L-линейное подпространство в 
. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.
5. В пространстве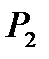 
многочленов степени не выше 2 оператор 
действует по правилу
(p(t)) = 
. Доказать, что - линейный оператор. Найти его матрицу в каноническом базисе и в базисе S=(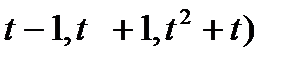
.
6.В пространстве 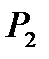многочленов степени не выше 2 оператор действует по правилу
(p(t)) = ((t2p(t-2)) 
. Доказать, что - линейный оператор. Найти его матрицу в каноническом базисе, найти ядро и образ оператор. Существует ли обратный оператор?
7.Линейный оператор 
в пространстве 
в базисе 
имеет матрицу 
. Найти собственные значения и собственные векторы оператора . Является ли он оператором простого типа? Если да, то указать базис из собственных векторов и матрицу оператора в этом базисе.
8.В пространстве 
оператор действует по правилу 
, 
. Показать линейность оператора, найти его матрицу в каноническом базисе и в базисе
S = { 
9.В пространстве 
линейный оператор 
- поворот на угол 
по часовой стрелке. Найти матрицу оператора 
в каноническом базисе. Найти образ вектора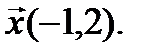 
Найти ядро и образ оператора. Существует ли обратный оператор? Является ли оператором простого типа?
10.Дана матрица Грама
= 
в базисе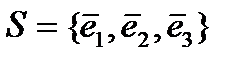 
. Ортогонализировать базис S.
Дата добавления: 2015-04-20; просмотров: 100 | Поможем написать вашу работу | Нарушение авторских прав |