
Читайте также:
|
 линейный оператор
линейный оператор  -поворот против часовой стрелки на угол
-поворот против часовой стрелки на угол  вокруг оси ОY.
вокруг оси ОY. 1) Найти матрицу оператора A в базисе  .
.
2) Найти образ вектора 
3) Найти ядро и образ оператора А.
4) Существует ли обратный оператор? Если да, то описать его действие.
5) Найти собственные значения и собственные векторы оператора  . Является ли он оператором простого типа?
. Является ли он оператором простого типа?
 линейный оператор
линейный оператор  - зеркальное отражение относительно оси ОХ.
- зеркальное отражение относительно оси ОХ. 1) Найти матрицу оператора A в базисе  .
.
2) Найти образ вектора 
3) Найти ядро и образ оператора А.
4) Существует ли обратный оператор? Если да, то описать его действие.
5) Найти собственные значения и собственные векторы оператора  . Является ли
. Является ли  оператором простого типа?
оператором простого типа?
 линейный оператор
линейный оператор  - зеркальное отражение относительно плоскости XОY.
- зеркальное отражение относительно плоскости XОY. 1) Найти матрицу оператора A в базисе  .
.
2) Найти образ вектора 
3) Найти ядро и образ оператора А.
4) Существует ли обратный оператор? Если да, то описать его действие.
5) Найти собственные значения и собственные векторы оператора  . Является ли
. Является ли  оператором простого типа?
оператором простого типа?
 линейный оператор
линейный оператор  - проекция на ось ОY.
- проекция на ось ОY. 1) Найти матрицу оператора  в базисе
в базисе  .
.
2) Найти образ вектора 
3) Найти ядро и образ оператора 
4) Существует ли обратный оператор? Если да, то описать его действие.
5) Найти собственные значения и собственные векторы оператора  . Является ли
. Является ли  оператором простого типа?
оператором простого типа?
5. В пространстве V 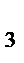 линейный оператор
линейный оператор  - проекция на плоскость YOZ.
- проекция на плоскость YOZ.
1) Найти матрицу оператора  в базисе
в базисе  .
.
2) Найти образ вектора 
3) Найти ядро и образ оператора 
4) Существует ли обратный оператор? Если да, то описать его действие.
5) Найти собственные значения и собственные векторы оператора  . Является ли
. Является ли  оператором простого типа?
оператором простого типа?
6. В пространстве V 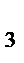 линейный оператор
линейный оператор  – гомотетия с коэффициентом к= -7.
– гомотетия с коэффициентом к= -7.
1) Найти матрицу оператора  в базисе
в базисе  .
.
2) Найти образ вектора 
3) Найти ядро и образ оператора 
4) Существует ли обратный оператор? Если да, то описать его действие.
5) Найти собственные значения и собственные векторы оператора  . Является ли
. Является ли  оператором простого типа?
оператором простого типа?
7. В пространстве P  оператор
оператор  действует по правилу
действует по правилу  p(t)=2
p(t)=2  .
.
1) Показать, что  линейный оператор в P
линейный оператор в P  .
.
2) Найти матрицу оператора в каноническом базисе пространства.
3) Найти ядро и образ оператора  .
.
4) Обратим ли оператор?  Если да, то указать явный вид обратного оператора.
Если да, то указать явный вид обратного оператора.
5) Найти собственные значения и собственные векторы оператора  .
.
Является ли оператор  оператором простого типа? Если да, то указать базис из собственных векторов и матрицу оператора в собственном базисе.
оператором простого типа? Если да, то указать базис из собственных векторов и матрицу оператора в собственном базисе.
8. В каноническом базисе пространства R  оператор
оператор  действует по правилу
действует по правилу
a) 
 =(3
=(3  ,
, 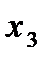 ,
,  );
);
1) Показать линейность оператора  .
.
2) Найти матрицу оператора в каноническом базисе пространства.
3) Найти ядро и образ оператора  .
.
4) Обратим ли оператор?  Если да, то указать явный вид обратного оператора.
Если да, то указать явный вид обратного оператора.
5) Найти собственные значения и собственные векторы оператора  .
.
Является ли оператор  оператором простого типа? Если да, то указать базис из собственных векторов и матрицу оператора в этом базисе.
оператором простого типа? Если да, то указать базис из собственных векторов и матрицу оператора в этом базисе.
9. Линейный оператор  в базисе (
в базисе ( ,
, 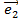 ,
,  ) задан матрицей A. Найти матрицу оператора
) задан матрицей A. Найти матрицу оператора  в базисе (
в базисе ( ,
,  ,
,  ).
).

 = -
= -  +
+  ,
,  = 2
= 2 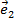 +
+  ,
,  =
=  -
- 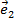 .
.
10.Является ли следующий оператор линейным оператором?
a)  =(
=( +
+ 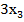 ,
,  +
+  ,
,  )
)
б)  =(
=( ,
,  +
+  ,
,  )
)
с)  =(
=(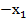 +
+  ,
,  +
+ 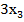 ,
,  +
+  )
)
Дата добавления: 2015-04-20; просмотров: 161 | Поможем написать вашу работу | Нарушение авторских прав |