Читайте также:
|
I Аксиоматика Гильберта евклидовой геометрии
1. Понятие аксиоматического метода построения геометрии.
2. Аксиоматика Гильберта I группа аксиом (аксиомы принадлежности), следствия из нее.
3. Аксиоматика Гильберта II группа аксиом (аксиомы порядка), следствия из I-II групп.
4. Аксиоматика Гильберта III группа аксиом (аксиомы конгруэнтности), следствия из I-III групп.
5. Аксиоматика Гильберта III группа аксиом (аксиомы непрерывности).
6. Понятие об абсолютной геометрии, примеры теорем абсолютной геометрии.
7. Пятый постулат Евклида, его эквиваленты.
II Геометрия Лобачевского
1. Аксиома Лобачевского. Параллельные прямые в геометрии Лобачевского. Признак параллельности прямых (без доказательства).
2. Теорема существования и единственности параллельных прямых.
3. Угол параллельности двух прямых. Функция Лобачевского.
4. Треугольники на плоскости Лобачевского: сумма углов, основной признак равенства треугольников.
5. Двупрямоугольники на плоскости Лобачевского. Двупрямоугольники Саккери, признак.
6. Существование оси симметрии двух параллельных прямых.
7. Симметрия параллельности прямых.
8. Расходящиеся прямые, признак расходящихся прямых.
9. Три вида пучков на плоскости Лобачевского. Окружность, ее свойства.
10. Три вида пучков на плоскости Лобачевского. Эквидистанта, ее свойства.
11. Три вида пучков на плоскости Лобачевского. Орицикл, его свойства.
Задачи к коллоквиуму по геометрии «Бакалавры математики» 3 семестр
I Аксиоматика Гильберта евклидовой геометрии
1. Доказать, что две прямые не могут иметь более одной общей точки.
2. Доказать, что если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат всеобщие точки этих плоскостей.
3. Доказать, что плоскость и не принадлежащая ей прямая могут иметь не более одной общей точки.
4. Доказать, что через прямую а и не принадлежащую ей точку С проходит единственная плоскость.
5. Доказать, что через две пересекающиеся прямые проходит единственная плоскость.
6. Доказать, что для любой точки А существуют по крайней мере две точки В и С такие, что А, В, С не лежат на одной прямой
7. Доказать, что для любых двух точек А и В существует хотя бы одна точка Р, лежащая между ними.
8. Доказать 1)Теорема о полуплоскости. Каждая прямая а, лежащая в плоскости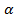 
, разбивает множество всех точек этой плоскости, не принадлежащих прямой а, на два непустых подмножества так, что любые две точки одного подмножества лежат по одну сторону от прямой а, а любые две точки из разных подмножеств лежат по разные стороны от прямой а.
2) Теорема о луче. Каждая точка О прямой l разбивает множество остальных точек этой прямой на два непересекающихся подмножества, так, что для любых двух точек одного подмножества точка О не лежит между ними, а для любых двух точек из разных подмножеств точка О лежит между ними.
9. Если А-С-В и А-D-С, то А-D-В.
10. Доказать, что если прямая а не проходит через вершины треугольника АВС, то она не может пересекать всех трех сторон треугольника.
11. Доказать, что на каждом отрезке, луче и прямой существуют бесчисленное множество точек. (Ук
12. Доказать, что если М – внутренняя точка угла АОВ, то луч ОМ – внутренний луч угла АОВ.
13. Доказать, что если точки М и N лежат на различных сторонах угла АОВ, то любая точка, лежащая между М и N, есть внутренняя точка угла АОВ.
14. Доказать, что любой внутренний луч угла пересекает любой отрезок с концами на разных сторонах угла. Без доказательства! Запомнить факт!!!
15. Доказать первый признак конгруэнтности треугольников (по двум сторонам и углу между ними).
16. Доказать: если конгруэнтны два угла, то конгруэнтны им смежные.
17. Доказать, что вертикальные углы конгруэнтны.
18. (Лемма о секущей). Доказать: если при пересечении двух данных прямых а и b секущей с накрест лежащие углы 1 и 2 конгруэнтны, то данные прямые не пересекаются.
19. Теорема о внешнем угле треугольника: Доказать: внешний угол треугольника больше любого внутреннего, не смежного с ним.
20. Доказать второй признак конгруэнтности треугольников (по стороне и прилежащим к ней углам).
21. Доказать 1У-й признак конгруэнтности треугольников: если в треугольниках АВС и А1В1С1 углы А и А1, В и В1 конгруэнтны, стороны АС и А1С1, то треугольники конгруэнтны.
22. Точка М является внутренней точкой треугольника АВС. Доказать, что угол АМВ больше угла АСВ.
23. Доказать, что углы при основании равнобедренного треугольника конгруэнтны.
24. Доказать, что биссектриса, медиана и высота равнобедренного треугольника, проведённые к основанию, совпадают.
25. Доказать, что через любую точку А можно провести единственную прямую, перпендикулярную прямой а. Рассмотреть два случая - точка А вне прямой а и на ней.
26. Пусть АОВ – данный угол, АН – перпендикуляр, проведённый из точки А к прямой ОВ. Тогда если угол АОВ острый, то точка Н лежит на луче ОВ, а если этот угол тупой, то точка Н лежит на продолжении луча ОВ.
27. Доказать, что у любого отрезка существует середина.
28. Доказать, что у любого неразвёрнутого угла существует биссектриса.
29. Доказать 3-й признак конгруэнтности треугольников (по трём сторонам).
30. Доказать признаки конгруэнтности прямоугольных треугольников:
а) по двум катетам; б) по катету и прилежащему острому углу; в) по катету и противолежащему острому углу; г) по гипотенузе и острому углу; д) по катету и гипотенузе.
Дата добавления: 2015-04-20; просмотров: 63 | Поможем написать вашу работу | Нарушение авторских прав |