Читайте также:
|
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
Скалярное произведение векторов 
, 
обозначается символом 
(порядок записи сомножителей безразличен, то есть 
).
Если угол между векторами , обозначить через 
, то их скалярное произведение можно выразить формулой
(1)
Скалярное произведение векторов , можно выразить также формулой
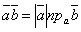, или 
.
Из формулы (1) следует, что 
, если - острый угол, 
, если - тупой угол; 
в том и только в том случае, когда векторы и перпендикулярны (в частности, , если 
или 
).
Скалярное произведение 
называется скалярным квадратом вектора и обозначается символом 
. Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля:
.
Если векторы и заданы своими координатами:
, 
,
то их скалярное произведение может быть вычислено по формуле
.
Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов
.
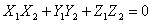Угол между векторами
, ,
дается формулой 
, или в координатах
.
Дата добавления: 2015-04-20; просмотров: 62 | Поможем написать вашу работу | Нарушение авторских прав |