
Читайте также:
|
1о. (k + l) 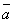 = k
= k 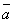 + l
+ l 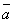 .
.
k ( 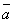 +
+  ) = k
) = k 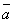 + k
+ k  .
.
2o. k (l 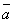 ) = (kl)
) = (kl) 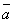 .
.
3o. 1× 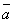 =
= 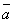 , (–1) ×
, (–1) × 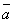 = –
= – 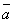 , 0 ×
, 0 × 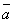 =
=  .
.
9 колинеарность векторов Свойства векторов.
Опр. 11. Два вектора 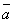 и
и  называются коллинеарными, если они расположены на параллельных прямых или на одной прямой.
называются коллинеарными, если они расположены на параллельных прямых или на одной прямой.
Нулевой вектор  коллинеарен любому вектору.
коллинеарен любому вектору.
Теорема 1. Два ненулевых вектора 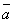 и
и  коллинеарны, Û когда они пропорциональны т.е.
коллинеарны, Û когда они пропорциональны т.е.  = k
= k 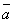 , k – скаляр.
, k – скаляр.
Опр. 12. Три вектора 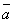 ,
,  ,
,  называются компланарными, если они параллельны некоторой плоскости или лежат в ней.
называются компланарными, если они параллельны некоторой плоскости или лежат в ней.
Теорема 2. Три ненулевых вектора 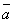 ,
,  ,
,  компланарны, Û когда один из них является линейной комбинацией двух других, т.е.
компланарны, Û когда один из них является линейной комбинацией двух других, т.е.  = k
= k 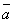 + l
+ l  , k,l – скаляры.
, k,l – скаляры.
10 раложение вектора по базису Постановка задачи. Найти разложение вектора  по векторам
по векторам
 .
.
План решения.
1. Искомое разложение вектора 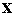 имеет вид
имеет вид
 .
.
2. Это векторное уравнение относительно  эквивалентно системе трех линейных уравнений с тремя неизвестными
эквивалентно системе трех линейных уравнений с тремя неизвестными

3. Решаем эту систему линейных алгебраических уравнений относительно переменных  и таким образом определяем коэффициенты разложения вектора
и таким образом определяем коэффициенты разложения вектора 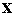 по векторам
по векторам  .
.
Замечание. Если система уравнений не имеет решений (векторы  лежат в одной плоскости, а вектор
лежат в одной плоскости, а вектор 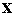 ей не принадлежит), то вектор
ей не принадлежит), то вектор 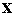 нельзя разложить по векторам
нельзя разложить по векторам  . Если же система уравнений имеет бесчисленное множество решений (векторы
. Если же система уравнений имеет бесчисленное множество решений (векторы  и вектор
и вектор 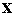 лежат в одной плоскости), то разложение вектора
лежат в одной плоскости), то разложение вектора 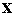 по векторам
по векторам  неоднозначно.
неоднозначно.
Задача 1. Написать разложение вектора 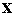 по векторам
по векторам  .
.

Имеем
 ,
,
или

Т.е. искомое разложение имеет вид
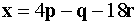 .
.
Дата добавления: 2015-04-20; просмотров: 153 | Поможем написать вашу работу | Нарушение авторских прав |