Читайте также:
|
Поняття визначеного інтеграла
Означення. Якщо існує скінченна границя інтегральних сум Sn при, яка не залежить ні від способу розбиття [a; b] на частини 
, ні від вибору точок, то ця границя називається визначеним інтегралом від функції на проміжку [a; b] і позначається: 
За означенням, визначений інтеграл 
— число, яке залежить від типу функції 
та проміжку [a; b]; він не залежить від того, якою буквою позначена змінна інтегрування: 
Властивості визначеного інтеграла
1) Якщо, то 
то 
2) Сталий множник можна виносити з-під знака визначеного інтеграла, тобто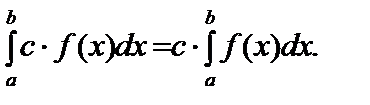 
3) Якщо 
та 
інтегровні на [a; b], то 
4) Якщо у визначеному інтегралі поміняти місцями межі інтегрування, то інтеграл змінить лише свій знак на протилежний, тобто 
5) Визначений інтеграл з однаковими межами інтегрування дорівнює нулю 
6) Якщо 
— інтегровна в будь-якому із проміжків: [a; b], [a; c], [с; b], то
7) Якщо f(x) — інтегровна та 
для 
Дата добавления: 2015-09-11; просмотров: 107 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Повторите всю процедуру (если еще кто-то остался) | | | Формула Ньютона—Лейбніца |