Читайте также:
|
Тут ми сформулюємо деякі важливі властивості визначеного інтеграла, які нам будуть потрібні у подальшому.
1. Величина визначеного інтеграла не залежить від позначення змінної інтегрування.
.
2. Якщо верхня межа інтегрування співпадає з нижньою, то інтеграл дорівнює нулю.
.
3. Від переставлення місцями меж інтегрування отримується інтеграл, який дорівнює даному з протилежним знаком.
.
4. Якщо функція 
інтегровна на максимальному з відрізків 
, 
, то справедлива рівність:
. (8.3.1)
Доведення. Припустимо спочатку, що 
. Розіб’ємо відрізок на частинні так, щоб точка 
була точкою розбиття, наприклад 
. Тоді
.
Цей факт добре ілюструється геометрично (рис. 8.4).
 |
Рис. 8.4
.
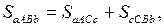
Формула (8.3.1) зберігає справедливість і у випадку, коли 
. Припустимо, наприклад що 
. Тоді згідно за попереднім:
.
На підставі властивості 3 маємо:
, і тоді:
, а звідси і випливає формула (8.3.1). Випадок 
розглядається аналогічно.
5. Сталий множник можна виносити за знак визначеного інтеграла:
.
6. Визначений інтеграл від суми (різниці) інтегровних функцій дорівнює сумі (різниці) інтегралів від цих функцій:
.
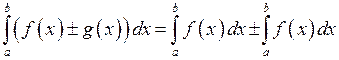7. Якщ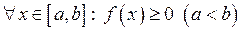о 
, то
.
8. Якщо 
, то
.
9. Якщо функція інтегровна на 
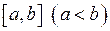, то
.
10. Якщо 
, то
.
Дійсно
.
11. Теорема (про середнє значення функції). Якщо функція неперервна на відрізку , то на цьому відрізку існує точка така, що буде виконана рівність
.
Доведення. Оскільки функція неперервна на відрізку , то згідно з 2-ю теоремою Вейєрштрасса (див. п.5.7) ця функція досягає на цьому відрізку свого найменшого та найбільшого значень 
. Тоді:
.
Або
.
Величина 
називається середнім значенням функції на відрізку . Внаслідок знову ж таки неперервності функції на відрізку на підставі 2-ї теореми Больцано-Коші (п.5.7) існує точка 
така, що 
, тобто
, звідки й випливає потрібне. Теорему доведено.
Дата добавления: 2015-09-11; просмотров: 159 | Поможем написать вашу работу | Нарушение авторских прав |