Студопедия
Главная страница | Контакты | Случайная страница

АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Застосування визначеного інтеграла

Читайте также:
  1. А) Характеристика методів візуалізації сечової системи, показання до застосування, їх можливості та обмеження.
  2. Б) Характеристика методів візуалізації статевої системи, показання до застосування, їх можливості та обмеження.
  3. Б. Технологія виготовлення вінірів із застосуванням кераміки "Duceram Low Fusing" ("Duceram", Німеччина).
  4. Визначення походження дитини, народженої в результаті застосування допоміжних репродуктивних технологій
  5. Виробнича структура: сутність, види та умови застосування в практичної діяльності.
  6. Властивості визначеного інтеграла
  7. Властивості визначеного інтеграла.
  8. Геометричні застосування визначеного інтеграла.
  9. Дайте визначення закону достатньої підстави, розкрийте його зміст та наведіть приклади його застосування.
  10. Досвід формування та вдосконалення основних механізмів консюмеризму в країнах ринкової економіки та можливість його застосування у вітчизняній практиці

А) Обчислення площ.

Якщо рівняння заданої лінії є , де , то площа криволінійної трапеції, яка обмежена знизу віссю ОХ, зверху кривою, праворуч та ліворуч прямими задаються формулою

Для випадку обчислення площ довільної плоскої фігури, обмеженої кривими,

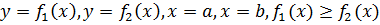
маємо формулу:

 

 

Ця формула є вірною для випадків, коли бічні сторони (одна чи обидві), стягуються у точки. Тоді за границі інтегрування беремо найменшу та найбільшу абсцису точок кривої, якщо вона одна, чи абсциси точок перетину двох кривих .

Нехай 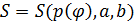та кривою (p, – полярні координати;p() – неперервна на [a;b]).

Тоді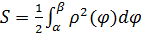

При розв’язку задач можна використовувати слідуючий алгоритм.

1. Зробити малюнок.

2. Знайти границі інтегрування та обчислити за формулою площу.

 

Приклад 5. Знайти площу фігури, обмеженої лініями та



Дата добавления: 2015-09-11; просмотров: 83 | Поможем написать вашу работу | Нарушение авторских прав
Глава 2 | Глава 3 | Глава 4 | Глава 5 | Глава 6 | Глава 7 |

lektsii.net - Лекции.Нет - 2014-2025 год. (0.007 сек.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав