Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Интегралы от квадратичных иррациональностей

Интегралы типа

1) ,

2) ,

3) ,

4) ,

5)

называются неопределенными интегралами от квадратичных иррациональностей (P_n (x) – алгебраический полином n ≥2).

Для нахождения интегралов 1) - 3) под радикалом выделяется полный квадрат

.

Затем делается подстановка

.

Пример 5. Найти интеграл

.

Решение _▼

.

.

Первый интеграл

.

Второй интеграл

.

.

^▲

Интегралы 4), т.е.

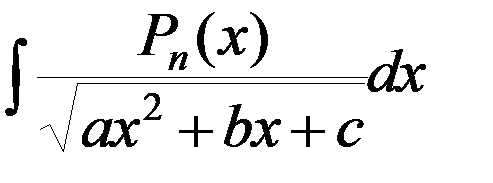
находятся по формуле Остроградского:

(1)

,

где Q_{n –1}(x) – полином степени n –1 с неопределенными коэффициентами; λ – число, подлежащее определению.

Для нахождения неопределенных коэффициентов и λ необходимо:

-продифференцировать формулу Остроградского по x;

-умножить обе части полученного равенства на ;

-сравнить коэффициенты при одинаковых степенях x.

Пример 6. Найти интеграл

.

Решение _▼ По формуле (1)

.

Выполняем дифференцирование

.

Применяем метод сравнения коэффициентов:

;

.

Система линейных уравнений:

; ; λ = 2.

.

^▲

Интегралы 5), т.е.

приводятся к интегралам 4) подстановкой

.