Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Замечание.

Во многих случаях нахождение наибольшего значения модуля первой производной (или второй производной для метода средних прямоугольников) подынтегральной функции на отрезке интегрирования является очень трудоемкой процедурой.

Поэтому можно действовать без использования неравенства для оценки абсолютной погрешности методов численного интегрирования. Хотя оценки предпочтительнее.

Для методов правых и левых прямоугольников можно использовать следующую схему.

Берем произвольное n (например, n = 5) и вычисляем приближенное значение интеграла. Далее удваиваем количество отрезков разбиения интервала интегрирования, то есть, берем n = 10, и вновь вычисляем приближенное значение определенного интеграла. Находим разность полученных приближенных значений для n = 5 и n = 10. Если абсолютная величина этой разности не превышает требуемой точности, то в качестве приближенного значения определенного интеграла берем значение при n = 10, предварительно округлив его до порядка точности. Если же абсолютная величина разности превышает требуемую точность, то вновь удваиваем n и сравниваем приближенные значения интегралов для n = 10 и n = 20. И так продолжаем до достижения требуемой точности.

Для метода средних прямоугольников действуем аналогично, но на каждом шаге вычисляем треть модуля разности полученных приближенных значений интеграла для n и 2n. Этот способ называют правилом Рунге.

Вычислим определенный интеграл из предыдущего примера с точностью до одной тысячной по методу левых прямоугольников.

Не будем подробно останавливаться на вычислениях.

Для n = 5 имеем , для n = 10 имеем .

Так как , тогда берем n = 20. В этом случае .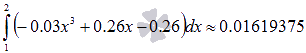

Так как 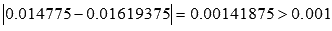, тогда берем n = 40. В этом случае .

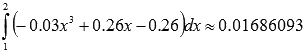Так как 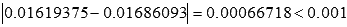, то, округлив 0.01686093 до тысячных, утверждаем, что значение определенного интеграла 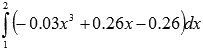равно 0.017 с абсолютной погрешностью 0.001.

К началу страницы

В заключении остановимся на погрешности методов левых, правых и средних прямоугольников более детально.

Из оценок абсолютных погрешностей видно, что метод средних прямоугольников даст большую точность, чем методы левых и правых прямоугольников для заданного n. В то же время, объем вычислений одинаков, так что использование метода средних прямоугольников предпочтительнее.

Если говорить о непрерывных подынтегральных функциях, то при бесконечном увеличении числа точек разбиения отрезка интегрирования приближенное значение определенного интеграла теоретически стремиться к точному. Использование методов численного интегрирования подразумевает использование вычислительной техники. Поэтому следует иметь в виду, что при больших n начинает накапливаться вычислительная погрешность.

Еще заметим, если Вам требуется вычислить определенный интеграл с некоторой точностью, то промежуточные вычисления проводите с более высокой точностью. Например, Вам требуется вычислить определенный интеграл с точностью до одной сотой, тогда промежуточные вычисления проводите с точностью как минимум до 0.0001.