
|
Читайте также: |
1. Если в условии Вейерштрасса 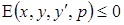 , а в условии Лежандра
, а в условии Лежандра 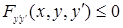 , то сформулированные условия являются достаточными условиями сильного максимума.
, то сформулированные условия являются достаточными условиями сильного максимума.
2. Условие Якоби в отдельности являются необходимым условием сильного экстремума, т.е. если решение уравнения Якоби  обращается в нуль при каком – либо значении
обращается в нуль при каком – либо значении 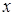 из интервала
из интервала  , то на экстремали
, то на экстремали 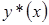 сильный экстремум не достигается.
сильный экстремум не достигается.
3. Условие Вейерштрасса в отдельности является необходимым, т.е. если функция Вейерштрасса в точках экстремали при некоторых 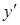 имеет противоположные знаки, сильный экстремум не достигается.
имеет противоположные знаки, сильный экстремум не достигается.
4. В случае когда функция 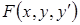 трижды дифференцируема по
трижды дифференцируема по 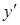 , условие Вейерштрасса можно заменить легко проверяемым условием Лежандра.
, условие Вейерштрасса можно заменить легко проверяемым условием Лежандра.
На основании изложенных необходимых и достаточных условий экстремума функционала опишем общую схему нахождения экстремума функционала.
Алгоритм нахождения экстремума в задаче (3)
1. Найти экстремаль (экстремали)  , удовлетворяющую уравнению Эйлера и заданным граничным условиям.
, удовлетворяющую уравнению Эйлера и заданным граничным условиям.
2. Проверить достаточные условия сильного и слабого экстремума на найденной экстремали. Если достаточные условия выполняются сделать вывод о достижении сильного или слабого минимума или максимума. Если достаточные условия не выполняются, учесть пп. 2 и 3 замечаний. В случае невыполнения условий Лежандра вывод об отсутствии экстремума сделать нельзя. Если достаточные условия экстремума выполняются, вычислить значение функционала на найденном решении.
Пример. Найти экстремум функционала
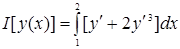 ,
, 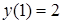 ,
, 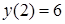 .
.
Решение.
1. Найдем экстремаль  , удовлетворяющую уравнению Эйлера и граничным условиям. Так как подынтегральная функция
, удовлетворяющую уравнению Эйлера и граничным условиям. Так как подынтегральная функция 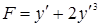 не зависит от
не зависит от 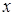 и
и 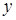 явно, то уравнение Эйлера имеет общее решение
явно, то уравнение Эйлера имеет общее решение  . Из граничных условий
. Из граничных условий

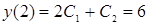
находим 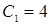 ,
, 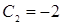 . В результате получаем экстремаль
. В результате получаем экстремаль  .
.
2. Проверим достаточные условия сильного экстремума:
а) для проверки условия Якоби составим уравнение Якоби (12). Так как на экстремали  производная равна
производная равна  и
и 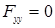 ,
,  ,
, 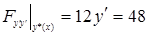 , то уравнение (12) имеет вид
, то уравнение (12) имеет вид 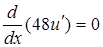 . Отсюда
. Отсюда 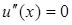 и
и  . Из условия
. Из условия 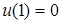 получаем
получаем 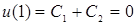 и
и 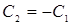 . Так как нетривиальное решение (
. Так как нетривиальное решение (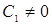 ) уравнения Якоби
) уравнения Якоби 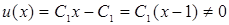 при
при 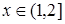 , то условие Якоби выполняется;
, то условие Якоби выполняется;
б) так как функция  трижды дифференцируема по
трижды дифференцируема по 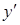 , то применим условие Лежандра. Поскольку
, то применим условие Лежандра. Поскольку 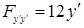 не сохраняет знака при любых
не сохраняет знака при любых 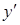 , то достаточные условия сильного максимума и минимума не выполняются, а вопрос о наличии сильного экстремума остается открытым.
, то достаточные условия сильного максимума и минимума не выполняются, а вопрос о наличии сильного экстремума остается открытым.
Проверим достаточные условия слабого максимума:
а) условие Якоби выполняется;
б) применим усиленное условие Лежандра. Так как 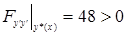 на экстремали
на экстремали  , то на ней достигается слабый минимум.
, то на ней достигается слабый минимум.
Найдем значение функционала:
 .
.
Пример. Найти экстремум функционала
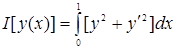 ,
,  ,
, 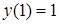 .
.
Решение.
1. Найдем экстремаль  , удовлетворяющую уравнению Эйлера и граничным условиям:
, удовлетворяющую уравнению Эйлера и граничным условиям: 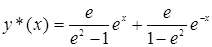 .
.
2. Проверим достаточные условия сильного экстремума:
а) для проверки условия Якоби составим уравнение Якоби (12). Так как 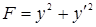 ,
, 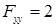 ,
, 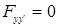 ,
, 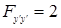 , то уравнение (12) имеет вид
, то уравнение (12) имеет вид 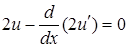 . Отсюда
. Отсюда  и
и  - общее решение. Из условия
- общее решение. Из условия 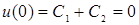 получаем
получаем 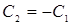 и
и  . Так как нетривиальное решение (
. Так как нетривиальное решение (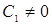 ) уравнения Якоби
) уравнения Якоби  при
при 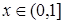 , то условие Якоби выполняется;
, то условие Якоби выполняется;
б) так как функция  трижды дифференцируема по
трижды дифференцируема по 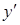 , то применим условие Лежандра. Поскольку
, то применим условие Лежандра. Поскольку  при любых
при любых 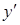 , то на кривой
, то на кривой  достигается сильный минимум. Очевидно на этой же кривой достигается и слабый минимум.
достигается сильный минимум. Очевидно на этой же кривой достигается и слабый минимум.
II. Функционалы 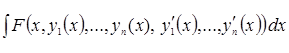 ,
,
Дата добавления: 2015-09-10; просмотров: 117 | Поможем написать вашу работу | Нарушение авторских прав |