Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Цикловые классы (типы).

Определение. Будем говорить, что перестановка PÎ{1,2,…,n} имеет тип < >, если P имеет k₁ циклов длины 1, имеет k₂ циклов длины 2, и т. д. Заметим, что 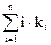= n.

Пусть С(k₁, k₂,…, k_n) есть число перестановок из n элементов типа k=< >.

Выясним, какова формула, определяющее общее число таких перестановок. Для того чтобы найти эту формулу выберем произвольную перестановку типа k и переставим ее элементы всеми возможными n! способами. Имеется две причины, в силу которых не все получившиеся в результате этой операции перестановки оказываются различными: (а) все циклы, в которых входят одни и те же элементы в одном и том же циклическом порядке, не отличаются друг от друга; (b) относительное расположение циклов в перестановке несущественно.

Как уже отмечалось, r-цикл может начинаться с любого из входящих в него r элементов, и, следовательно, имеется возможность (в силу a) получить r дубликатов этого цикла. Общее число дубликатов составит 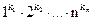. Далее, если число r-циклов равно k_r, то их можно переставлять k_r! способами, поэтому (в силу b) окажется дубликатов k₁!· k₂!·…· k_n!.

Следовательно,

С(k₁, k₂,…, k_n)= 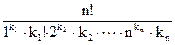, где k₁ +2k₂+…+nk_n=n. (1)

Примеры.

1. Шесть перестановок из трех элементов распадаются на три цикловых классов следующим образом:

тип	перестановки	число
< >	(123); (132)
< >	(12)(3); (13)(2); (1)(23)
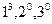< >	(1)(2)(3)

2. Число перестановок типа < 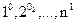> равно n!/n= (n-1)!

Эта формула проверяется с помощью следующего соображения: в n-цикле первым элементом по условию является 1, а для расстановки оставшихся n-1 элементов существует (n-1)! возможностей.

3. Единственная перестановка типа < > совпадает с тождественной перестановкой.

Производящая функция чисел С(k₁, k₂,…, k_n) должна иметь вид многочлена от многих переменных, так как n видов циклов должны независимыми. Этот факт выражается соотношением

С_n(t₁, t₂,…, t_n)=ΣС(k₁, k₂,…, k_n)

Следовательно, с учетом (1)

С_n(t₁, t₂,…, t_n)= (2)

Сумма (2) берется по всем неотрицательным целым числам от k₁ до k_n таким, что k₁ +2k₂+…+nk_n=n, или, что то же самое, по всем разбиением числа n. Функция С_n(t₁, t₂,…, t_n) называется цикловым индикатором (указателем) симметрической группы.

Для первых значений n имеем:

С₁(t₁) =t₁

С₂(t₁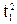, t₂)= +t₂

С₃(t₁, t₂, t₃)= +3t₁t₂+2t₃

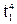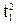С₄(t₁, t₂, t₃, t₄)= +6 t₂+3 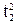+8t₁t₂+6t₄

Удобно принять С₀=1.

Из сопоставления соотношений (2) и (6) следует

С_n(t₁, t₂,…, t_n)=A_n(1; t₁, t₂, 2! t₃,…, (n-1)!t_n)=

= Y_n(t₁, t₂, 2! t₃,…, (n-1)!t_n) (3)

Последнее выражение является следствием соотношения (2а) при соответствующем изменении буквенных обозначений. В силу (5), это то самое, что и основное порождающее тождество:

exp(uC)= (t₁, t₂,…, t_n)uⁿ/n!= exp(ut₁+u²t₂/2+u³t₃/3+…) (3a)

весьма удобное для дальнейшей работы.

Свойства С_n(t₁, t₂,…, t_n)

1. С_n(1, 1,…, 1)= n!

Это согласуется с (3а), так как

exp(ut₁+u²t₂/2+u³t₃/3+…) =exp(log(1-u)^-1)=(1-u)^-1 =1+u+u²+…

2. (тождество Коши)

следует из 1, учитывая (2)

3.Введенная ранее производящая функция числа перестановок n-го порядка C_n(t) может быть получена из С_n(t₁, t₂,…, t_n), если все t_r приравнять t, т.е.

С_n(t)=С_n(t, t,…, t)

Следовательно, из (3а) имеем

exp(uC(t))= = exp(t(u+u²/2+u³/3+…) = exp(t·log(1-u)^-1=(1-u)^-t=

=1+ 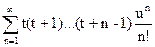(4)

что согласуется с ранее полученными результатами для С_n(t).