Читайте также:
|
Definite Integral
Lecture 34 Definite Integral. Basic Properties of Definite Integral
Definition Let 
be a continuous function defined on 
divide the interval by the points
from 
to 
into 
subintervals ( not necessarily equal width) such that when 
, the length of each subinterval will tend to zero.
 |
for 
. If
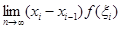
exists and is independent of the particular choice of 
and 
, then we have
(1)
For equal width, i.e. divide 
into equal subintervals of length, i.e. 
, we have
.
Choose 
and 
, hence
.
Definition If for a function the limit (1) exists, then we say the function is integrable on .
Theorem If a function is continuous on , then it is integrable on that interval.
Remark
R1 The value of the definite integral of a given function is a real number, depending on its lower and upper limits only, and is independent of the choice of the variable of integration, i.e.
.
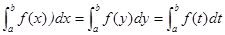R2 
(by definition).
R3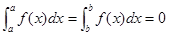 
(by definition)
Basic Properties of Definite Integrals
If 
are integrable functions on then
(a) 
for some constant k.
(b) 
.
(c) If 
(Even Function) then
(d) If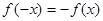 
(Odd Function), then
(e) Let 
, then 
.
Theorem (Comparison of two integrals)
If 
, then 
.
Theorem If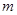 
and 
are the smallest and greatest values of a function on , 
and 
, then
.
Дата добавления: 2015-09-11; просмотров: 99 | Поможем написать вашу работу | Нарушение авторских прав |