
Читайте также:
|
НЕОПРЕДЕЛЕННЫй ИНТЕГРАЛ. 
Основные свойства неопределенного интеграла.
1).  ;
;
2).  ;
;
3).  ;
;
4).  , где
, где 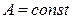
5)  - свойство инвариантности
- свойство инвариантности
Таблица основных производных и интегралов

| 
| 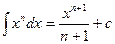

| 

|

| 
|


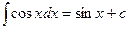

|


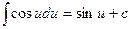

|

| 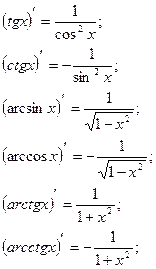
| 



| 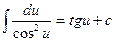



|
методы интегрирования.
1. Интегрирование подстановкой
 .
.
2. Интегрирование методом интегрирования по частям
 .
.
Типы интегралов, берущиеся интегрированием по частям:

| |

| |
| «круговой интеграл» | 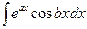 , , 
|
Интегрирование рациональных алгебраических функций:
1.Если подынтегральная дробь неправильная, то нужно выделить целую часть.
2. Если дробь правильная, то нужно применить разложение правильной дроби на простейшие дроби:

Интегрирование тригонометрических функций:
1. Используемые формулы:
 ,
,  ,
,  .
.
Примеры:  ,
,  ,
,  .
.
2.Используемые формулы:
 ,
,
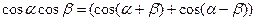 ,
,

Пример:  .
.
3.Универсальная тригонометрическая подстановка:
 - подстановкой
- подстановкой  , тогда
, тогда  ,
,
 ,
, 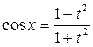 ,
, 
Пример:  .
.
4. Если под интегралом  и
и  содержатся только в четных степенях, то лучше применять подстановку:
содержатся только в четных степенях, то лучше применять подстановку:
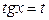 , тогда
, тогда  ,
,  ,
,  ,
, 
5.  - подстановкой
- подстановкой 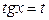 , тогда
, тогда  ,
,  .
.
Дата добавления: 2015-09-10; просмотров: 81 | Поможем написать вашу работу | Нарушение авторских прав |