
Читайте также:
|
Задание
Дана исходная функция: F(x) = 8Cos(x) – x – 6
Найти приближенное значение корня с точностью E=10-5 методом Эйткена-Стеффенсона. Построить график заданной функции в Excel для определения интервала, в котором лежит значение корня. Подставить найденное значение корня в исходное уравнение и определить достигнутую точность решения.
Описание заданного численного метода
Методом Эйткена-Стеффенсона решаются нелинейные уравнения вида
x = f(x)
путем многократного применения итерационной формулы
xn+1 = f(xn)
до тех пор, пока соблюдаются условие
½ xn+1 - xn ½³ e,
где e - заданная погрешность вычисления корня.
Алгоритм решения следующий:
1 Задаем начальное приближение xn = x 0 (значение x 0, рядом с которым лежит корень, выбирается по графику функции y = F(x)), построенному в Excel).
2 Находим первое x1 = f(x 0 ) и второе x2 = f(x 1 ) приближения.
3 Вычисляем 
4 Проверяем условия: ½ xn+ 1 - xn ½> e и x 0 – 2x 1 +x 2¹ 0. Если эти условия соблюдаются, то идем к п. 1, в противном случае процесс прекращается и получаем значении корня, равное x n+1.
Метод Эйткена-Стеффенсона при сложных F(x) имеет ускоренную сходимость (по сравнению с методом простых итераций). Однако при простых функциях F(x) время решения практически не уменьшается, т.к. число дополнительных операций в этом методе существенно больше, чем в методе простых итераций.
График исходной функции
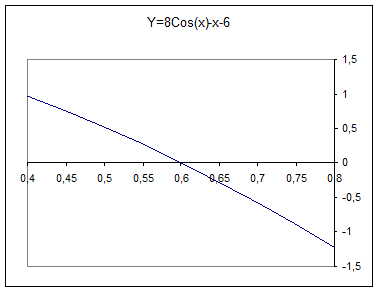
Из графика видно, что корень заданной функции лежит в районе 0,6. Выбираем значение x0 = 0,55.
Дата добавления: 2015-09-10; просмотров: 75 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Регламент финала конкурса в номинации | | | Схемы программ |