Читайте также:
|
Задания к пакету MATLAB. Вычисления с плавающей точкой
Задание 1. Решение систем линейных алгебраических уравнений
Задания 1-5.
Табл. 1
| номер задания | Матричная операция и оператор языка заданий пакета MATLAB | номер тестового примера |
inv - обращение квадратной невырожденной ( )-матрицы
| ||
| обращение матрицы с помощью оператора \ - "матричного деления" | ||
| обращение симметричной ()-матрицы с помощью оператора chol - разложения (Холесского) на множители
| ||
| обращение матрицы с помощью оператора lu - LU-разложения на множители ()-матрицы
| ||
| обращение матрицы с помощью оператора qr - QR-разложения на множители ()-матрицы
|
1. a) Написать подпрограмму формирования тестовой матрицы A и ее обратной (
) по соответствующим формулам.
б) Написать подпрограмму численного нахождения обратной матрицы указанным методом.
Требуемое численное значение обратной матрицы получать, последовательно решая системы Axi = ei относительно столбцов xi матриц из матричного уравнения AX=E, где X - искомая обратная матрица, E - единичная. В заданиях 3-5 для этого сначала, с помощью указанной операции, найти матричное разложение, а затем решить n систем линейных уравнений методом исключения, используя специальный вид получившихся в разложении матриц. (Не пользоваться специальными командами MATLAB для решения СЛАУ). Примечание. В задании 3 сформированная матрица должна быть симметричной и положительно определенной.
2. Средствами пакета МATLAB построить графики функций:
a) T = T(n), T(n) - время, затраченное на обращения матрицы, n - ее порядок.
б) F=F(cond), 
;
cond - число обусловленности для данной задачи;
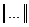- любая из норм, доступных в пакете;
X - найденное численное значение обратной матрицы;
- известное точное решение.
в)линейную аппроксимацию функции F по методу наименьших квадратов. Функции б) и в) должны быть построены на одном графике. Объяснить результаты.
3. Для n =5 получить аналитические представления для A и A-1 , используя символьные возможности пакета MATLAB и написанную подпрограмму формирования матриц (см. п.1 а)).
Задания 6-10.
Табл. 2
| номер задания | Матричная операция и оператор языка заданий пакета MATLAB | номер тестовойматрицы |
| решение системы с помощью оператора inv - обращения квадратной невырожденной ()-матрицы
| ||
| решение системы с помощью оператора \ - "матричного левого деления" | ||
| решение системы с помощью оператора chol - разложения Холесского на множители | ||
| решение системы с помощью оператора lu - LU- разложения на множители ()-матрицы
| ||
| решение системы с помощью оператора qr - QR- разложения на множители ()-матрицы
|
1. a) Написать подпрограмму формирования тестовой матрицы A и аналитического решения исследуемой системы (
).
б) Написать подпрограмму численного решения системы указанным методом.
В заданиях 8-10 численное решение системы A = b, где - заранее известное решение, b - соответствующий ему вектор правой части получать следующим методом. Сначала найти разложение матрицы, а затем решить системы линейных уравнений методом исключения, используя специальный вид получившихся в разложении матриц. (Не пользоваться специальными командами MATLAB для решения СЛАУ). Например,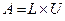 
, 
, Ly = b, Ux = y.
Примечание. В задании 8) матрица системы должна быть симметричной и положительно определенной.
2. Средствами пакета МATLAB построить графики функций:
а) T = T(n), T(n) - время решения системы, n - ее порядок.
б) F = F(cond), 
, где
cond - число обусловленности для данной задачи;
- любая из норм, доступных в пакете;
- найденное численное решение;
- известное точное решение. (Взять произвольный вектор и построить b = A )
в)линейную аппроксимацию функции F по методу наименьших квадратов. Функции б) и в) должны быть построены на одном графике. Объяснить результаты.
3. Для n =5 получить аналитическое представление для A, используя символьные возможности пакета MATLAB и написанную подпрограмму формирования матрицы (см. п.1 а)).
Задания 11-20
Строчки и столбцы приведенной табл. 3 содержат названия сравниваемых методов. На пересечении строк и столбцов расположен номер варианта / номер тестовой матрицы.
1. a) Написать подпрограмму формирования тестовой матрицы A и аналитического решения исследуемой системы ().
б) Написать подпрограммы численного решения системы указанными методами. Для указанных преподавателем вариантов из табл. 3:
Табл. 3
| inv | lu | qr | \ | chol | |
| inv | 11/15 | 12/17 | 20/13 | 13/18 | |
| lu | 14/19 | 15/8 | 16/21 | ||
| qr | 17/22 | 18/20 | |||
| \ | 19/17 |
провести сравнение "численных методов" решения систем A = b, реализованных по формулам:
а) inv обращение матрицы
б) lu A=L*U, L*U*x=b
L*y=b
U*x=y
в) qr A=Q*R, Q*R*x=b
R*x=Q'*b
г) \ "матричное деление"
д) chol A=R*R', R*R'*x=b
R*y=b
R'*x=y
Примечание. В случае сравнения с методом Холесского, матрица должна быть симметричной и положительно определенной. Численное решение системы A = b, где - заранее известное решение, b - соответствующий ему вектор правой части получать следующим методом. Сначала найти разложение матрицы, а затем решить системы линейных уравнений методом исключения, используя специальный вид получившихся в разложении матриц. (Не пользоваться специальными командами MATLAB для решения СЛАУ).
2. Средствами пакета МATLAB построить графики функций:
а) T = T(n), T(n) - время решения системы, n - ее порядок(для двух "методов" на одном графике);
б) F = F(cond), (для двух "методов" на одном графике), где:
;
сond - число обусловленности для данной задачи;
- любая из норм, доступных в пакете;
x – найденное приближенное решение;
- точное решение. (Взять произвольный вектор и построить b=A ).
в)линейную аппроксимацию функции F по методу наименьших квадратов. Объяснить результаты.
3. Для матрицы размерностью 5x5 получить аналитическое представление A, используя символьные возможности пакета MATLAB и написанную подпрограмму формирования матрицы.
Дата добавления: 2015-09-10; просмотров: 188 | Поможем написать вашу работу | Нарушение авторских прав |