Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Исходные данные к РГР № 3

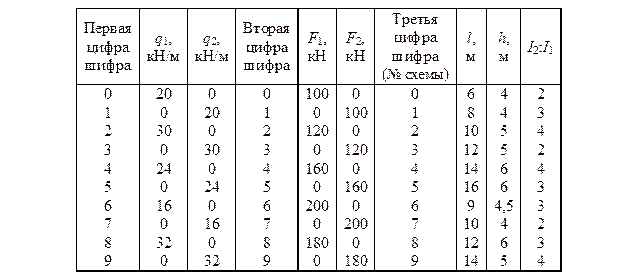
Последовательность расчета

4.1. Изобразить в масштабе расчетную схему рамы с указанием размеров и приложить заданную нагрузку.

4.2. Определить степень статической неопределимости рамы

n _с = 3К – Ш,

где n _с – степень статической неопределимости или число так называемых “лишних” связей, К – число замкнутых контуров, а Ш – число простых шарниров в расчетной схеме, включая опорные, или число связей, необходимых для полного защемления всех узлов расчетной схемы.

Рис. 4.1. Расчетные схемы к РГР № 4

4.3. Выбрать две статически определимые и геометрически неизменяемые основные системы путем удаления “лишних” связей, приложив по их направлению соответствующие неизвестные X ₁, X ₂,… X_n. Более рациональную из этих основных систем использовать для дальнейшего расчета.

4.4. Записать в общем виде систему канонических уравнений метода сил применительно к данной расчетной схеме.

4.5. Показать расчетные схемы основной системы при последовательном загружении единичными безразмерными силами, приложенными по направлениям удаленных связей. На расчетных схемах показать опорные реакции, определить их и построить эпюры изгибающих моментов .

4.6. Показать расчетную схему основной системы при загружении ее внешней нагрузкой, определить опорные реакции и построить в основной системе эпюру изгибающих моментов .

4.7. Определить коэффициенты при неизвестных системы канонических уравнений

,

где m - число участков интегрирования.

4.8. Определить свободные члены системы канонических уравнений

.

4.9. Подставить найденные значения коэффициентов и свободных членов в систему канонических уравнений и решить ее относительно неизвестных X_i.

4.10. Построить эпюры изгибающих моментов от действительных значений реакций в удаленных связях. Для этого все ординаты эпюр (i = 1… n) умножаются на соответствующую величину X_i.

4.11. Построить эпюру изгибающих моментов в заданной расчетной схеме на основании принципа независимости действия сил

.

4.12. Произвести деформационную проверку расчета. Для этого берется любая другая статически определимая основная система (например, вторая из выбранных в п. 4.3), в которой строится эпюра изгибающих моментов от одновременного действия на нее всех единичных сил, приложенных по направлениям удаленных связей. При правильно выполненном расчете должно выполняться условие

.

Деформационная проверка будет выполняться и в том случае, если в приведенной формуле вместо 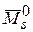использовать любую из эпюр 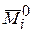основной системы.

Примечание. Деформационная проверка имеет смысл, если выбранная для проверки новая основная система дает эпюры 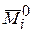, линейно независимые (не подобные) эпюрам , использованным в расчете.

4.13. Построить эпюру поперечных сил Q_F в заданной расчетной схеме, используя дифференциальную зависимость Q_F = d M /d x.

4.14. Построить эпюру продольных сил N_F. Значения продольных сил в стержнях рамы определяются из условий равновесия ее узлов. К вырезанным узлам кроме неизвестных продольных сил прикладываются найденные поперечные силы и известные узловые нагрузки.

4.15. Произвести проверку равновесия системы. При выполнении данного пункта рекомендуется рассмотреть два сечения: сечение, проведенное по опорным связям (рассматривается равновесие всей рамы), и сечение, проведенное в любом месте расчетной схемы (рассматривается равновесие отсеченной части). При правильном построении эпюр для любой отсеченной части системы должны выполняться уравнения равновесия 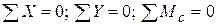, где c - любая точка на плоскости.