Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Расчет закрытой цилиндрической косозубой передачи.

Исходные данные:

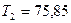Н·м Н·м

кВт кВт

2.3.1 Выбираем марку материала шестерни и колеса.

Шестерня: сталь 40х [3, табл. 8.8]

Твердость поверхности: HRC₁=55

Твердость сердцевины: 28 HRC

=800 МПа – предел текучести

=1000 МПа – предел прочности

термообработка: закалка.

Колесо – сталь 40х

Твердость поверхности: HB₂=245

=550 МПа

=850 МПа

Термообработка: улучшение.

2.3.2. Определяем допускаемые напряжения в зубчатой передаче.

а) Допускаемые контактные напряжения

, (2.29)

где - предел выносливости при нулевом цикле

- коэффициент безопасности [3, табл. 8.9]

- коэффициент долговечности

Если передача работает длительно, то

Для шестерни:

Для колеса: [3, табл. 8.9]

МПа

МПа

Косозубая передача рассчитывается на прочность по среднему допускаемому контактному напряжению:

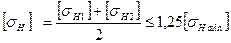(2.30)

Условие не соблюдается, тогда

МПа

б) Допускаемые напряжения изгиба

, (2.31)

где 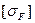- допускаемое напряжение изгиба

- предел выносливости при изгибе, МПа

- коэффициент безопасности

-коэффициент долговечности, =1

-коэффициент, учитывающий влияние двухстороннего приложения нагрузки, т.к. передача не реверсивная, =1.

[σ]_F1=550 МПа

[σ]_F2=1,8*HB₂=1,8*245=441 МПа

S_F1=S_F2=1, 75 [3,табл. 8.8.]

шестерня: [σ_F]₁= МПа

колесо: [σ_F]₂= МПа

2.3.3. Определяем межосевое расстояние передачи

, (2.32)

где u_з.п. -передаточное отношение

Т₂-крутящий момент на валу колеса,Н*м

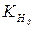— коэффициент неравномерности нагрузки по длине зуба,

— коэффициент ширины колеса относительно межосевого расстояния;

= 0,4 [3, табл. 8.4]

[3, стр. 179]

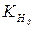=1,04 [3, стр. 136]

=0,5 (u+1)=1,3

Рассчитываем межосевое расстояние:

Принимаем межосевое расстояние [3, стр. 136]

2.3.4 Определяем ширину колеса

(2.33)

2.3.5. Определяем нормальный модуль передачи

, (2.34) где - коэффициент ширины колеса относительно модуля

[3, с. 137, таб. 8.5]

Принимаем нормальный модуль передачи; [3, с.116]

2.3.6. Определяем угол наклона зубьев

(2.35)

Где - коэффициент осевого перекрытия

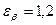[3, с.146 ]

2.3.7. Определяем число зубьев шестерни и колеса.

Находим торцевой модуль: (2.36)

Находим общее число зубьев шестерни и колеса

, (2.37)

Число зубьев шестерни:

, (2.38)

Округляем до ближайшего целого числа:

Число зубьев шестерни:

, (2.39)

где — число зубьев шестерни;

— число зубьев колеса

2.3.8. Уточним значение угла наклона зубьев по межосевому расстоянию

(2.40)

2.3.9. Уточним значение торцевого модуля и определяем диаметры (делительные впадин и выступов)

(2.41)

Делительный диаметр:

(2.42)

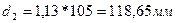
Диаметр вершин зубьев:

(2.43)

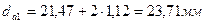
Диаметр впадин зубьев:

(2.44)

2.3.10. Выполняем проверочный расчет по контактным напряжениям

(2.45)

где — коэффициент повышения прочности косозубых цилиндрических передач по контактным напряжениям;

(2.46)

-коэффициент неравномерности нагрузки одновременно зацепляющихся пар зубьев

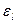-коэффициент торцевого перекрытия

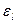= (2.47)

=

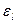Определить окружную скорость:

(2.48)

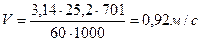
По значению 9-ой степени точности (3,табл. 8.2.) получаем

=1,13 [3, табл. 8.7. c.149]

В нашем случае принимаем:

Sin2L=0.6428

(2.49)

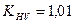[3, таб..8.3]

[3, рис. 8.15]

446МПа

Определим отклонение:

(2.50)

<4%

4.11 Выполняем проверочный расчет по напряжениям изгиба

(4.25)

где — коэффициент формы зуба

— окружная сила

— коэффициент расчетной нагрузки

— коэффициент повышения прочности косозубых передач по направлениям изгиба

(4.26)

где — коэффициент неравномерности одновременно зацепляющихся пар зубьев

— коэффициент, учитывающий влияние наклона контактной линии к основанию зуба

По и 9-ой степени точности определяем [3, стр. 149]

(4.27)

(4.28)

H

— коэффициент расчетной нагрузки;

(4.29)

где — коэффициент концентрации нагрузки;

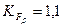[3, c.129]

— коэффициент динамической нагрузки;

[3, c.132]

Определим эквивалентное число зубьев шестерни и колеса для нахождения 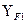и

(4.30)

Тогда [3, стр. 140]

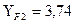
Составляем соотношение

< <

4.12Определяем силы, действующие в зацеплении

-радикальная сила

- осевая сила

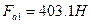
- нормальная сила