Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Метод вариации произвольной постоянной.

Общее решение однородной системы можно записать в виде

, где - фундаментальная матрица системы, - вектор произвольных постоянных.

Будем искать решение неоднородной системы в том же виде, варьируя вектор произвольных постоянных:

.

Вычисляем производную и подставляем в уравнение неоднородной системы:

,

,

Так как фундаментальная матрица удовлетворяет уравнению однородной системы, то 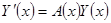. Поэтому в предыдущем уравнении (как и всегда в методе вариации) сокращается пара слагаемых. Получаем уравнение

. Так как фундаментальная матрица не вырождена (), то отсюда получаем уравнение для определения вектора :

.

Интегрируя, получаем

(здесь предполагается, что при вычислении интеграла вектор констант не добавляется, он уже добавлен в виде вектора ).

Подставляя в , имеем

() .

Здесь в полном соответствии с теоремой о структуре общего решения неоднородной системы первое слагаемое представляет собой общее решение однородной системы, а второе слагаемое – частное решение неоднородной системы.