Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Лекции 19-20. Нормальные системы дифференциальных уравнений.

Система дифференциальных уравнений – это система уравнений относительно независимой переменнойx, функций этой переменной и их производных . Система может быть записана в общем виде

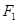( )=0

....................................................................

( )=0

Порядок этой системы равен .

Пользуясь теоремой о неявной функции, можно разрешить систему уравнений относительно старших производных и записать ее в каноническом виде:

( )

..................................................................................

( )

Теорема. Любое дифференциальное уравнение, разрешенное относительно старшей производной, можно свести к системе дифференциальных уравнений первого порядка.

Доказательство. Рассмотрим дифференциальное уравнение n-ого порядка

. Обозначим . Дифференциальное уравнение n-ого порядка удалось свести к системе n дифференциальных уравнений первого порядка

Применяя эту теорему, можно от канонического вида системы дифференциальных уравнений перейти к системе дифференциальных уравнений первого порядка - нормальному виду системы.

................

.........................................................................................

.................

Получена система из дифференциальных уравнений первого порядка.

Удобнее нормальную систему дифференциальных уравнений (систему в нормальной форме) записывать в виде:

.................................. (покоординатная форма)

или в виде

, где (векторная форма).

Пример. Эти уравнения сводятся к нормальной системе

()

()

Оказывается, не только дифференциальное уравнение n- ого порядка сводится к системе n дифференциальных уравнений первого порядка – нормальной системе, но и нормальная система может быть сведена к одному дифференциальному уравнению.

Теорема. Пусть задана система n дифференциальных уравнений первого порядка

..................................

Обозначим

...................................

Потребуем, чтобы функция была бы дифференцируемой по совокупности переменных. Потребуем, чтобы определитель

Тогда система n дифференциальных уравнений эквивалентна одному дифференциальному уравнению n-ого порядка.

Доказательство. Метод доказательства называется методом исключения переменных и применяется на практике при сведении системы к одному уравнению. Продифференцируем :

1) Построим алгоритм метода исключения.

Пусть - решения системы (), тогда уравнения системы представляют собой тождества

...................................

Получены выражения производных

,

,

,

...

.

Из этих уравнений можно выразить через , так как определитель системы этих уравнений

Подставим выражения через в последнее уравнение . Так как - решения системы , то они являются и решениями полученного уравнения. Следовательно, система сведена к одному уравнению n-ого порядка.

2) Покажем эквивалентность решений. Предположим, что - решения полученного уравнения, покажем, что - решения системы.

, . Обозначим . . Обозначим , и т.д. . Обозначим .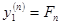

Приравниваем полученные здесь функции введенным ранее, сокращая первые и вторые слагаемые, получаем систему уравнений

.....................................

.

Определитель этой системы равен , следовательно, в качестве единственного решения системы имеем . Поэтому решения эквивалентны. Теорема доказана.

Пример.

,

Функция называется общим решением системы, если

1. для любого - решение системы

2. для произвольных начальных условий найдется , что .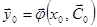

Если зафиксировать в общем решении, получим частное решение системы.