
Читайте также:
|
1. Приращением (вариацией)  аргумента функционала
аргумента функционала  называется разность между двумя функциями:
называется разность между двумя функциями:
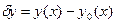 (4)
(4)
где  – некоторая фиксированная функция,
– некоторая фиксированная функция,  – произвольная функция.
– произвольная функция.
В окрестности функции 
 .
.
2. Функционал  называется непрерывным, если малому изменению
называется непрерывным, если малому изменению  соответствует малое изменение v.
соответствует малое изменение v.
Если в функционал входит 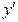 , то малости
, то малости 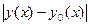 обычно недостаточно, необходима малость
обычно недостаточно, необходима малость  и т.д.
и т.д.
Кривые 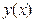 и
и  близки в смысле близости k-го порядка, если все модули разностей
близки в смысле близости k-го порядка, если все модули разностей 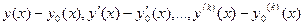 - малы.
- малы.



 Рис.3. Кривые, близкие в смысле близости 1-го порядка.
Рис.3. Кривые, близкие в смысле близости 1-го порядка.


 Рис. 4. Кривые, близкие в смысле близости 0-го порядка.
Рис. 4. Кривые, близкие в смысле близости 0-го порядка.
Функционал  непрерывен при
непрерывен при 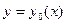 в смысле близости k-го порядка, если для любого
в смысле близости k-го порядка, если для любого 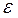 >0 существует
>0 существует 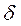 >0 такие, что
>0 такие, что
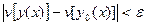 при
при 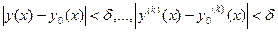 для
для 
Это означает, что малому приращению аргумента соответствует малое приращение функционала.
3. Функционал называется линейным, если выполняется условие:
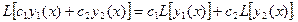 (5)
(5)
(линейные функционалы обозначаются: 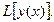 ).
).
4.
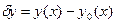 - вариация аргумента.
- вариация аргумента.
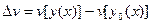 - приращение функционала.
- приращение функционала.
Сопоставим с дифференциальными исчислениями:
Функция 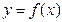 ,
, 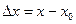
 (
(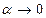 когда
когда 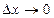 )
)
Дифференциалом  называется главная часть приращения
называется главная часть приращения 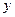 , линейная по
, линейная по 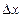 ,
,  .
.
По аналогии, для приращения функционала, можно записать:
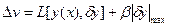 ,(
,(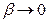 при
при  ) (6)
) (6)
Тогда главная часть приращения 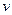 , линейная по
, линейная по  , называется вариацией функционала и обозначается
, называется вариацией функционала и обозначается 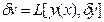 .
.
Альтернативный способ записи: 
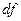

Аналогично этому вариация функционала:

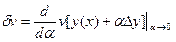 (7)
(7)
5. Функционал  имеет max (min) на функции
имеет max (min) на функции  , если для любой функции
, если для любой функции  вблизи
вблизи  разность между
разность между  и
и  неотрицательна (не положительна):
неотрицательна (не положительна):
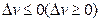
Теорема. Если функционал имеет max (min) (экстремален) на кривой  , то на этой кривой вариация функционала равна нулю. (По аналогии с функциями, где производная или дифференциал равны нулю).
, то на этой кривой вариация функционала равна нулю. (По аналогии с функциями, где производная или дифференциал равны нулю).
Доказательство.
Все функции близкие к функции  можно представить в виде
можно представить в виде  . При
. При 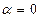 мы имеем экстремальную кривую
мы имеем экстремальную кривую 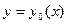 , тогда функционал
, тогда функционал 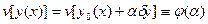 . Этот функционал имеет экстремум при
. Этот функционал имеет экстремум при 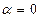 , поэтому можно исследовать на экстремум не
, поэтому можно исследовать на экстремум не  , а функцию
, а функцию 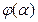 , а эта функция экстремальна в точке, где
, а эта функция экстремальна в точке, где 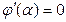 или
или 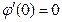 .
.
 , т. е.
, т. е. 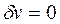 на
на  .
.
Дата добавления: 2015-09-10; просмотров: 88 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Примеры. | | | Уравнение Лагранжа-Эйлера. |