Читайте также:
|
Рассмотрим функционал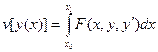 
(кривая закреплена)
(8)
где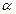 
- параметр, 
– экстремальная кривая, 
– семейство функций.
При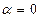 
функционал достигает экстремума. Тогда 
.
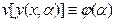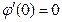- условный экстремум.
- функционал, записанный как функция.
из равенства (8) 
.
второе слагаемое возьмем по частям.
т.к. 
(функция закреплена в этих точках).
, потому что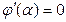 
Так как 
- произвольная, а интеграл равен нулю при любом 
(9)
Уравнение (9) называется уравнением Лагранжа-Эйлера и позволяет найти функцию .
Уравнение (9) является дифференциальным уравнением 2-го порядка с граничными условиями 
, т. е. для нахождения надо решать краевую задачу.
Уравнение (9) можно записать в форме:
В обозначении частных производных знак «штрих» можно опустить.
(10)
Пример. Длина кривой соединяющей две точки.
Найти длину кривой (или выбрать кривую) соединяющую две точки с минимальной длиной.
Попробуем использовать уравнение (10)
, 
, 
, 
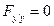1. 
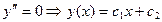
2. проверим выражение 
воспользуемся уравнением (9).
0=0 – это равенство выполняется при любых функциях , т.е. задача не имеет решения, т. е. нет экстремума.
Данный функционал имеет значения на всех кривых .
Функционал не зависит от кривой, т. е. он равен константе.
По формуле (9):
, 
, 
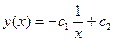
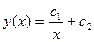
Зададим начальные условия: 
, воспользовавшись ими, находим константы: 
, 
, получим 
Для того, чтобы исследовать дает полученная кривая max или min, необходимо:
1. взять любую другую кривую, проходящую через данные точки;
2. вычислить значение функционала на обеих кривых;
3. сравнить полученные значения; если значение полученной кривой меньше (больше), чем значение выбранной, то полученная кривая – min (max).
Дата добавления: 2015-09-10; просмотров: 150 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Некоторые определения. | | | Пример. |