Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Примеры.

Вариационное исчисление.

Определение. Если М – множество функций , и каждой функции , принадлежащей М, ставится в соответствие число v, то переменная величина v называется функционалом, зависящим от функции .

Функционал записывается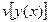

Определение функционала можно сопоставить с определением функции, где каждому числу ставится в соответствие число.

Примеры.

1. Всем четным функциям ставится в соответствие 1;

2. Всем нечетным функциям ставится в соответствие 1;

3. Всем ни четным, ни нечетным функциям ставится в соответствие 0.

Рассмотрим непрерывные функционалы.

1.Длина кривой.

Найдем длину кривой 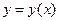на промежутке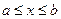

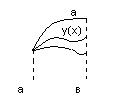
рис. 1. Семейство кривых

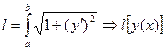(1)

Длина кривой – это функционал, зависящий от функции .

2.Площадь поверхности.

Рис. 2. Площадь поверхности

Найдем площадь поверхности .

(2)

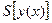является функционалом, если задана функция .

Для разных значений z число S различно.

Таким образом, мы подошли к рассмотрению функционалов, зависящих от функций нескольких переменных:

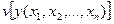
Аналогично можно рассматривать функционалы, зависящие нескольких функций:

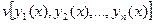
В качестве примера, запишем длину кривой, заданной в пространстве параметрическими уравнениями:

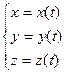
тогда длина кривой в трехмерном пространстве:

(3)

Формулы, которые мы будем изучать, имеют интегральную форму. Именно такие формулы встречаются в физических и геометрических приложениях. Такие формулы приводят к дифференциальным уравнениям.