Читайте также:
|
Формула Тейлора позволяет приближенно представить любую функцию с помощью многочлена (полинома) п -й степени, причем ошибка без труда находится и оценивается.
Теорема Тейлора. Брук Тейлор (Taylor, 1685-1731) - английский математик.
Пусть функция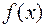 
имеет в точке а и некоторой ее окрестности производные порядка п +1. Пусть х - любое значение аргумента из указанной окрестности, 
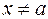. Тогда между точками а и х найдется точка x такая, что справедлива следующая формула:
(2.7.1)
Без доказательства.
Замечание. При п =0 получаем частный случай - формулу Лагранжа:
.
Таким образом, можно сказать, что формула Тейлора есть обобщение формулы Лагранжа на случай п производных.
Формула (2.7.1) называется формулой Тейлора, а последнее слагаемое в ней - остаточным членом в форме Лагранжа. Таким образом,
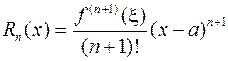. (2.7.2)
Приведем еще одну форму записи остаточного члена - в форме Пеано (Пеано Джузеппе, Peano, 1858-1932).
Покажем, что если производная (п +1)-го порядка функции 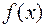, т.е. 
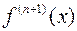ограничена в окрестности точки а, то остаточный член 
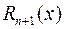является бесконечно малой более высокого порядка, чем 
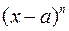при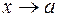 
. Для этого вычислим отношение этих двух бесконечно малых:
,
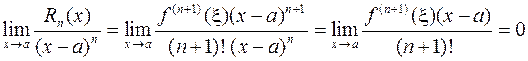т.к. функция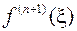 
ограничена, а 
при 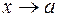, а произведение бесконечно малой функции на ограниченную есть бесконечно малая. Таким образом,
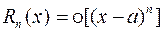при 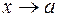. (2.7.3)
Это форма Пеано для остаточного члена. Тогда формула Тейлора примет вид:
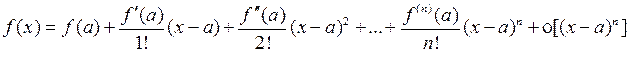
При 
формула Тейлора (2.7.1) превращается в формулу Маклорена:
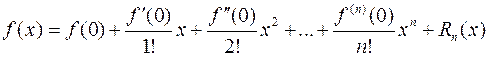(2.7.4)
Остаточный член имеет вид:
1) в форме Лагранжа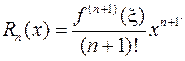 
;
2) в форме Пеано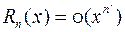 
.
Пример 1. Разложить многочлен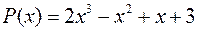 
по степеням 
.
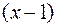Имеем: а =1. Напишем формулу Тейлора для 
:
.
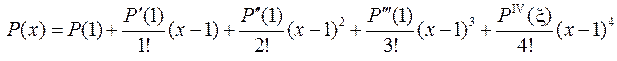Найдем производные в точке а =1.
;
; 
;
; 
;
; 
;
.
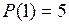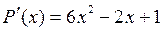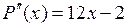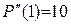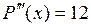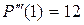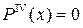Четвертая производная равна нулю, поэтому остаточного члена не будет. Подставляем в многочлен Тейлора:
.
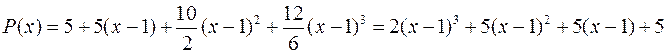Пример 2. Написать формулу Маклорена для функции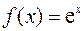 
().
Эта функция имеет производные любого порядка на (-¥, +¥). При этом:
,
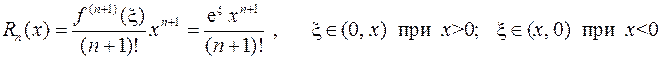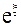- число.
.
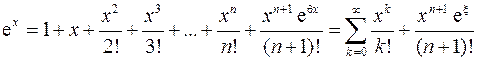Дата добавления: 2015-09-10; просмотров: 151 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| КУПАНИЕ | | | медиана |