Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Теоретические предпосылки к работе

К основным параметрам, характеризующим механические свойства твердых материалов, относятся модуль Юнга и модуль сдвига, связывающие величины продольных и сдвиговых напряжений с величинами продольных и соответственно сдвиговых деформаций в условиях одноосного нагружения материала. Для нахождения упругих модулей таких материалов, как горные породы, металлы, дерево, оргстекло и т.д. может быть применен резонансный метод, при применении которого в данной работе используют продольные колебания стержней, выполненных из исследуемого материала.

Так, если в стержне из упругого материала возбуждать продольные колебания, то они будут распространяться вдоль стержня в виде плоских волн с так называемой стержневой скоростью С_СТ:

(2.1)

где Е - модуль Юнга материала стержня, Н/м²;

r - плотность материала стержня, кг/м³.

В связи с тем, что стержень представляет собой ограниченное тело, в нем возможно возникновение явления резонанса и образование стоячих волн. Стоячие волны образуются в результате сложения двух одинаковых, но бегущих в противоположных направлениях гармонических волн и записываются следующим образом:

, (2.2)

где x - смещение сечения стержня относительно равновесного состояния;

k=w/С_СТ - волновое число.

Стоячая волна характеризуется особыми точками (сечениями), амплитуда в которых максимальна (пучности) и минимальна (узлы). Характер распределения амплитуды смещения в стоячей волне вдоль стержня зависит от граничных условий на концах стержня и в местах жесткого закрепления какого-либо сечения стержня, где будут наблюдаться узлы. На свободных концах стержня будут возникать пучности. В остальных местах стержня амплитуда будет зависеть от вида граничных условий, от длины стержня l и от частоты колебаний стержня f.

В случае если оба конца стержня свободны или закреплены, то первый резонанс или основная мода возникают при условии l=l/2. При увеличении частоты возбуждения будут возникать новые резонансы на частотах, кратных частоте основной моды.

При закреплении стержня в центре резонанс наблюдается при условии, что по длине стержня укладывается нечетное число полуволн (рис. 2.1):

, (2.3)

где l - длина стержня;

l=C_СТ / f - длина волны в стержне;

n - номер гармоники, n =1,3,5,7

Определяя экспериментально величину резонансных частот f_n, можно рассчитать стержневую скорость C_СТ на основании формулы (2.3) и при известном значении плотности материала стержня может быть определен модуль Юнга:

Е=r С²_СТ=r . (2.4)

Рис.2.1

При заданной величине коэффициента Пуассона модуль сдвига материала стержня равен

. (2.5)

Резонансный метод позволяет определять также величины, характеризующие потери в материале или в горных породах. Для этого измеряется ширина резонансной кривой (рис. 2.2.) на уровне 0,707, от амплитуды на резонансе А_Р путем определения значений частот и и резонансной частоты . На основании полученных величин можно рассчитать основные характеристики потерь в материале стержня:

- логарифмический декремент затухания

, (2.6)

где - частота собственных колебаний образца породы, ;

и - частоты колебаний, соответствующие амплитудам 0,7 до и после резонанса, ;

- временной коэффициент затухания

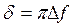; (2.7)

- добротность резонансной системы

Q = ; (2.8)

- коэффициент потерь

. (2.9)

Рис. 2.2.

Рис. 2.3.