Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Кінетичне рівняння для вільних електронів

Знайдемо закон зміни середнього імпульсу електронів у металі під дією зовнішніх сил. Нехай (t) - середній імпульс електронів в момент часу t, нехай f - сила, що діє на кожен електрон. Знайдемо тоді (t + dt), середній імпульс через час dt.

З імовірністю електрон на протязі часу буде рухатись без зіткнень, і тому його імпульс, згідно другому закону Ньютона, збільшиться на dt. З імовірністю електрон зазнає зіткнення десь на інтервалі dt, після цього "втратить пам'ять" (тобто його середній векторний імпульс стане рівний нулю), і буде набувати додаткового імпульсу dt протягом інтервалу dt' між моментом зіткнення і кінцем інтервалу dt(dt’<dt). Середнє значення імпульсу електрона в момент t + dt можна знайти як математичне очікування цих двох ситуацій:

(t + dt) =()( (t)+ dt+ (0+ )

Відкинемо величини другого порядку малості:

(t + dt) = (t)+ dt + 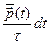, звідси

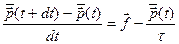,отже

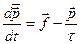—це рівняння для руху тіла у в'язкому середовищі. Величина -

грає роль в'язкого опору.

Приклад 1 . Легкопереконатись (методом розділення змінних), що розв’язок рівняння 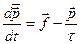має вигляд:

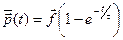
якщо початковий середній імпульс .

Фізичний зміст цього розв'язку очевидний. Поки середній імпульс електронів малий, "в'язкий опір" теж малий, так що електрони прискорюються майже рівномірно . Коли середня швидкість електронів зростає до певної величини, сила в'язкого опору компенсує зовнішню силу і електрони рухаються в середньому з постійною швидкістю (стаціонарний режим).

Аналогія: людина, що падає з великої висоти, не розкриваючи парашута, досягає максимальної швидкості біля 60 м/с, яка далі не збільшується, тому що при цій швидкості сила опору повітря рівна силі тяжіння. Приклад 2. , тобто зовнішня сила гармонічна.

1 спосіб: фізично очевидно, що гармонічна сила повинна викликати гармонічні коливання, але зі зсувом по фазі (відставанням), викликаним дією "в'язкого опору". Тому шукаємо розв'язок у вигляді . Підстановка цієї залежності у кінетичне рівняння дає:

.

Використаємо факт лінійної незалежності функцій cos і sin: якщо

, для будь-якого t, то звідси випливає, що А=0, В=0.

для будь-якого t.

Звідсивипливає, що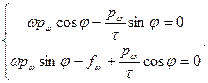

Легко бачити, що тоді ( - зсув по фазі,

- амплітуда коливань.

2 спосіб: отримаємо той самий результат через комплексні величини. Нехай де - комплексна амплітуда.

, звідси . Врахуємо, що = .

Тоді

Отже,

Цей результат дає можливість ввести поняття комплексної провідності, яка використовується для характеристики поведінки електронного газу під дією гармонічної електричної сили:

Присутність уявної частини означає зсув по фазі між струмом і напруженістю поля. Комплексна провідність буде використана зараз для опису розповсюдження електромагнітних хвиль у металі.