Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

И непротиворечивости теории первого порядка.

Логическое следование. Теоремы корректности и непротиворечивости для теорий первого порядка. Элементарная теория данной интерпретации. Полные теории первого порядка. Формулировка теоремы Гёделя о полноте исчисления предикатов без равенства (существование модели для непротиворечивой теории и доказуемость общезначимых формул).

1. Запишите на языке логики предикатов определения:

1) линейно упорядоченного множества,

2) ограниченной функции,

3) четной функции,

4) периодической функции,

5) возрастающей функции на множестве M.

2. Пользуясь полученными в предыдущем упражнении формулами, запишите высказывания:

1) упорядоченное множество не является линейным,

2) функция не является ограниченной,

3) функция не является четной,

4) функция не является периодической,

5) функция не является возрастающей на множестве M.

4. Докажите, что следующие формулы являются тавтологиями логики предикатов:

5. Докажите, что в логике предикатов выполняются следующие логические следования, выражающие на языке логики предикатов пятнадцать правильных аристотелевых силлогизмов

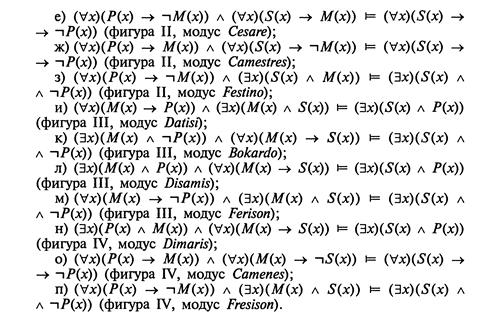
Литература:[2,3,4,7,16,17,19,21,23,24,25]

Учебно-методическая литература:[2]