
Читайте также:
|
Полученная система соотношений (1.4)... (1.8) может рассматриваться как базисная модель оценки характеристик производительности. Входящий в модель параметр l является усредненной характеристикой работы пользователей за экраном, а параметр m — функцией технических параметров ЭВМ и характеристик прикладных программ САПР. Эта связь должна быть установлена с помощью соотношений, называемых интерфейсными моделями.
С помощью базисных моделей можно исследовать характер поведения системы при изменении ее входных параметров. Графики зависимости m и tp от числа терминалов САПР при разных соотношениях l /m изображены на рис. 1.3 соответственно сплошной и штриховой линиями.
Рассмотрим модель (рис. 1.4), на которой проиллюстрируем методы повышения вычислительной эффективности марковских моделей.
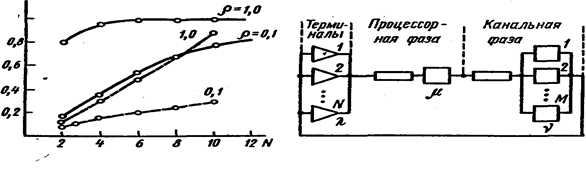
Рис. 1.3. Зависимости пропускной Рис. 1.4. Структура модели
ной способности и времени реакции
от числа терминалов
В модели отдельно представлены центральный процессор (процессорная фаза) и подсистема обмена (канальная фаза), включающая в себя селекторные каналы и накопители на магнитных дисках. Пусть каждый запрос пользователя требует решения задачи в процессоре и обмена информацией между НМД и ОП, осуществляемой посредством селекторного канала. В зависимости от конкретного варианта подключения НМД к селекторным каналам и распределения задач пользователей по НМД получаются разные формализованные схемы подсистемы обмена. Рассмотрим один из вариантов, состоящий в том, что имеется общая очередь заявок к совокупности селекторных каналов, из которой заявки выбираются в порядке их поступления. В системе N терминалов и М селекторных каналов. Среднее время обдумывания Тобд =1/l; среднее время решения задачи в процессоре Треш =1/m; среднее время обмена Тобм = 1/n.
Если принять допущение, что время решения задачи, время обмена и время обдумывания представляют собой независимые случайные величины, имеющие экспоненциальные распределения, то изменение состояния системы во времени может быть описано марковским процессом.
Опишем состояние системы в момент времени t вектором x (t)= x1 (t),x2 (t)), где x1 (t) — число заявок на терминальной фазе (число пользователей, получивших ответ системы и непосредственно работающих за экраном); x 2(t) — число заявок на процессорной фазе.
 |
Рис. 1.5. Граф переходов (а) и структура фрагмента графа (б)
Тогда число заявок на канальной фазе в момент t (число задач, осуществляющих обмен НМД—ОП и ожидающих обмена) равно N – (x1(t) + x2 (t)).
Граф переходов марковского процесса для частного случая N = 3, М = 2 изображен на рис. 1.5, а, а структура фрагмента графа переходов для общего случая — на рис. 1.5, б, где c1 = x1 (t) = i; c2 = min { M, N — (i +j)}.
Исходя из структуры графа переходов в соответствии с общим правилом можно записать систему линейных алгебраических уравнений относительно стационарных вероятностей состояния. Записать решение этой системы в явном виде не удается, поэтому в процедуре расчета выходных параметров, осуществляемого с помощью ЭВМ, надо предусмотреть блок формирования матрицы коэффициентов системы уравнений и обращение к стандартной программе решения системы линейных алгебраических уравнений. Зная значения pij, можно вычислить
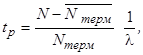
где
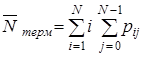 .
.
Дата добавления: 2014-12-15; просмотров: 110 | Поможем написать вашу работу | Нарушение авторских прав |