
Читайте также:
|
Записать систему уравнений в матричном виде. __ Т __(Р´) = Р × λ
 |  | ||||||
 |  | ||||||

 Р0´ - 3·λ 3·λ 0 0
Р0´ - 3·λ 3·λ 0 0
Р1´ = Р0 Р1 Р2 Р3 × µ -(µ+2·λ) 2·λ 0
Р2´ 0 µ -(µ+λ) λ
Р3´ 0 0 µ -µ
Задание № 3.
Выявить особенности матрицы.
- квадратная,
- сумма элементов строки равна нулю,
- элементы диагоналей имеют закономерности, что означает возможность формализации.
2. Матричное представление уравнений Колмогорова=Чепмена
Задание № 6.
Для условий задачи № 1 разработать графическую модель системы массового обслуживания в переходных вероятностях и записать уравнения в матричном виде.
|
|
|
| ||||||||||||||||||
 | |||||||||||||||||||||
 |  |  | |||||||||||||||||||
|
|
| |||||||||||||||||||
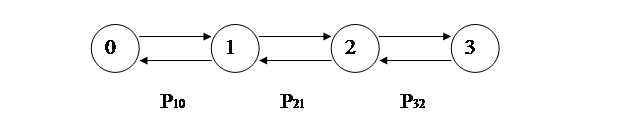
Р0 = (1,0,0,0)
РК = РК-1 × Р[ N×N]



 P00 P01 P02 P03 P00 P01 0 0
P00 P01 P02 P03 P00 P01 0 0
Р[4×4] = P10 P11 P12 P13 = P10 P11 P12 0
P20 P21 P22 P23 0 P21 P22 P23
P30 P31 P32 P3 0 0 P32 P33

P00 = 1 - P01
P11 = 1 - P10 - P12
P22 = 1 - P21 - P23
P33 = 1 - P32
 Рij = 1 – exp (-λij · t)
Рij = 1 – exp (-λij · t)
λij – элементы матрицы интенсивностей λ,
t  – интервал времени (время перехода, шаг интегрирования).
– интервал времени (время перехода, шаг интегрирования).
Дата добавления: 2014-12-15; просмотров: 64 | Поможем написать вашу работу | Нарушение авторских прав |