Читайте также:
|
Физическое воспитание – составная часть всех воспитательных систем. Сегодня обществу требуется физически крепкое молодое поколение, которое может достойно занять свое место в социуме, а именно – переносить нагрузки технологизации и информатизации общества, отличаться высокой «сопротивляемостью» организма к переменчивым условиям внешней среды, наличием качеств, необходимых для успешной профессиональной деятельности и др.
Задачи физического воспитания:
· содействие полноценному развитию организма, укрепление здоровья, правильное физическое развитие;
· повышение умственной и физической работоспособности;
· развитие и совершенствование природных двигательных качеств;
· обучение новым видам движений;
· формирование гигиенических навыков;
· воспитание нравственных качеств (смелости, настойчивости, решительности, дисциплинированности, ответственности, коллективизма);
· формирование потребности в систематических занятиях физкультурой и спортом;
· развитие стремления быть здоровым, бодрым, доставлять радость себе и окружающим.
Векторы и линейные операции над ними
Аудиторные задачи:
1) АВСДЕК – правильный шестиугольник, причем 
. Выразить через 
и векторы 
2) Даны векторы 
и 
. Коллинеарны ли векторы 
и 
?
3) Даны координаты трех последовательных вершин параллелограмма А (1,2,5), В (-4,3,6), С (-1,-2,7). Найти координаты вершины Д.
4) Могут ли векторы 
, 
, 
быть сторонами треугольника?
5) Лежат ли точки А(2,5,-1), В(1,-5,-15) и С(-2,1,3) на одной прямой?
6) Определить при каких значениях a, b векторы 
, 
коллинеарны?
7) Пусть векторы и неколлинеарны и 
. Найти α и β и доказать коллинеарность векторов 
и 
.
8) Установить, в каких случаях тройки векторов 
, 
и 
будут линейно зависимы, и в том случае, когда это возможно, представить вектор как линейную комбинацию векторов и :
а) ={5; 2; 1}; ={–1; 4; 2}; ={–1; –1; 6};
б) ={6; 4; 2}; ={–9; 6; 3}; ={–3; 6; 3};
в) ={6; –18; 12}; ={–8; 24; –16}; ={8; 7; 3}.
Домашнее задание:
1) Точки K и L служат серединами сторон BC и CD параллелограмма ABCD. Выразить векторы и 
через векторы 
и 
.
2) Найти координаты точки, симметричной точке А (-2,0,7) относительно точки В( 5,-1,2).
3) Найти расстояние между концами векторов 
, 
, если векторы отложены от точки А (-3, 2, 5).
4) Даны: | | = 13; | | = 19 и | + | = 24. Вычислить | – |.
5) Выяснить, являются ли четыре точки А (3,-1,2), В (1,2,-1), С( -1,1,3), Д (3,-5,3) вершинами трапеции.
6) Даны векторы 
, 
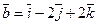и 
. Выяснить, образуют ли эти векторы линейно зависимую систему. В случае положительного ответа найти эту зависимость..
7) Даны векторы 
, 
и 
. Разложить вектор 
по векторам 
, и 
.
8) (*) Доказать, что для любых заданных векторов 
, 
и 
векторы + , + и 
- 
компланарны.
Дата добавления: 2014-12-15; просмотров: 103 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Виды воспитания, их значение в спорте | | | Правила дифференцирования |