Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Теории подобия.

Первая теорема подобия утверждает, что для явлений (объектов, процессов), подобных в том или ином смысле, существуют одинаковые критерии подобия — идентичные по форме алгебраической записи и равные численно безразмерные степенные комплексы (произведения или отношения) определенных групп физических факторов, характеризующих эти явления. Формулируя необходимые условия существования подобия (одинаковые критерии подобия у подобных явлений), первая теорема, однако, не указывает способы установления подобия и способы его реализации при построении моделей.

Вторая теорема подобия, чаще встречающаяся под названием р-теоремы, имеет следующий вид: всякое полное уравнение физического процесса, записан­ное в определенной системе единиц, может быть представлено функциональной зависимостью между критериями подобия, полученными из участвующих в процессе параметров. Вторая теорема устанавливает возможность представления интеграла дифференциального уравнения физического процесса не как функции параметров процесса и системы, в которой протекают эти процессы, а как функция соответствующим образом построенных некоторых безразмерных величин — критериев подобия.

Практически более удачная формулировка третьей теоремы, предложенная в последнее время, имеет вид, отвечающий реальным задачам создания различных моделей. Эта формулировка состоит из трёх положений.

Положение 1. Создание модели возможно, если критерии подобия (безразмерные комплексы), составленные из величин, характеризующих только ее системные (материальные) параметры, равны соответствующим критериям изучаемой системы-оригинала.

Положение 2. В созданной, согласно положению 1, модели осуществление процессов, подобных оригиналу, возможно, если критерии подобия, содержащие только параметры процессов, входящих в условия однозначности и в том числе начальные условия (параметры исходного режима, возмущений и отклонений), в модели и оригинале соответственно одинаковы.

Положение 3. Осуществление модели согласно формулировкам 1 и 2 возможно в сколь угодно сложных анизотропных, нелинейных или имеющих вероятностно заданные параметры системах при условии одновременного соблюдения соответствующих дополнительных положениях.

В гидромеханике важнейшими критериями подобия являются: Число Рейнольдса: , Определяет, в частности, переход от ламинарного режима к турбулентному.

Число Маха: .

Число Фруда: 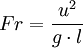. В этих примерах

ρ — плотность жидкости или газа, l— характерный размер, u — скорость течения, μ — динамический коэффициент вязкости, - кинематический коэффициент вязкости, a* — местная скорость распространения звука в движущейся среде.