Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Практическое применение уравнения Бернулли. Изменение пьезометрического и скоростного напоров при сужении и расширении сечения потоков.

Закон Бернулли позволяет объяснить эффект Вентури: в узкой части трубы скорость течения жидкости выше, а давление меньше, чем на участке трубы большего диаметра, в результате чего наблюдается разница высот столбов жидкости ∆ h; бо́льшая часть этого перепада давлений обусловлена изменением скорости течения жидкости, и может быть вычислена по уравнению Бернулли. Эффект Вентури является следствием действия закона Бернулли, которому соответствует уравнение Бернулли, определяющее связь между скоростью v жидкости, давлением p в ней и высотой h, на которой находится рассматриваемый элемент жидкости, над уровнем отсчёта: где ρ — плотность жидкости, а g — ускорение свободного падения. Если уравнение Бернулли записать для двух сечений потока, то будем иметь: . Для горизонтального потока средние члены в левой и правой частях уравнения равны между собой, и потому сокращаются, и равенство принимает вид: то есть при установившемся горизонтальном течении идеальной несжимаемой жидкости в каждом её сечении сумма пьезометрического и динамического напоров будет постоянной. Для выполнения этого условия в тех местах потока, где средняя скорость жидкости выше (то есть, в узких сечениях), её динамический напор увеличивается, а гидростатический напор уменьшается (и значит, уменьшается давление).

19.Число Рейнольдса. С какой целью его необходимо знать? Размерности величин входящих в формулу для его определения.

Критерий Рейно́льдса (Re) — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье — Стокса[1]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.

где ρ — плотность среды, кг/м3; v — характерная скорость, м/с; D_г — гидравлический диаметр, м; η — динамическая вязкость среды, Н·с/м2; ν — кинематическая вязкость среды, м2/с (ν= η/ ρ), Q — объёмная скорость потока; A — площадь сечения трубы. Для каждого вида течения существует критическое число Рейнольдса, Re_кр, которое, как принято считать, определяет переход от ламинарного течения к турбулентному. При Re<Re_кр течение происходит в ламинарном режиме, при Re>Re_кр возможно возникновение турбулентности. исло Рейнольдса есть мера отношения сил инерции, действующих в потоке, к силам вязкости. Плотность в числителе выражения 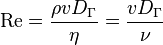характеризует инерцию частиц, отклонившихся от движения по прямой, а вязкость в знаменателе показывает склонность жидкости препятствовать такому отклонению. Также число Рейнольдса можно рассматривать как отношение кинетической энергии жидкости к потерям энергии на характерной длине (ввиду внутреннего трения).

Если у потока число Рейнольдса достаточно большое (выше критической величины), то жидкость можно рассматривать как идеальную. В таком случае вязкостью можно пренебречь.