Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Решения уравнения Шредингера

Нахождение точного решения требует решения уравнения Шредингера с потенциальной энергией (1), которое имеет вид

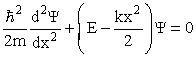
Трудности решения связаны со слагаемым, содержащим x². Приведем здесь только результаты вычислений. Анализ показывает, что, как и в случае с прямоугольной потенциальной ямой, волновые функции, являющиеся решением этого уравнения, будут непрерывными и конечными не при всех значениях энергии E, а лишь при дискретном наборе значений:

где n принимает значения 0, 1, 2,.... Отметим, что энергетические уровни гармонического осциллятора в отличие от случая прямоугольной потенциальной ямы расположены на одинаковом энергетическом расстоянии друг от друга ΔE = hυ.

Важной особенностью решения является наличие так называемых нулевых колебаний - колебаний с энергией, соответствующих значению квантового числа n = 0. Отличие от нуля минимальной энергии осциллятора характерно для всех квантовых систем и является следствием соотношения неопределенностей (см. оценку выше). В реальных квантовых системах, например, кристаллах, эти колебания сохраняются, как показывает опыт, даже при температурах, близких к абсолютному нулю, когда, казалось бы, все тепловое движение должно прекратиться. Опыты по рассеянию света кристаллами при низких температурах это подтверждают. Велика роль нулевых колебаний и в объяснении природы сил молекулярных взаимодействий (пример ниже) и других молекулярных явлений.

Первые три волновых функции гармонического осциллятора выглядят так:

Здесь введено обозначение x₀² = h/(4π²mυ).

Графики этих волновых функций представлены на рисунке ниже.

Пунктиром показаны границы, между которыми совершала бы колебания классическая частица. Значения a₀ отличаются для разных n, так как от n зависит энергия Е (~E^1/2). Очевидно, что при малых значениях квантового числа n плотность вероятности нахождения частицы, определяемая квадратом модуля волновой функции ψ₀(x)², кардинальным образом отличается от плотности вероятности обнаружения классического осциллятора: в основном состоянии максимальное значение вероятности приходится на центр, модуль волновой функции для всех квантовых чисел n имеет наибольшие значения между классическими точками поворота и экспоненциально убывающие "хвосты" вне этих точек.

Определим для основного состояния, как велика вероятность P обнаружения частицы вне пределов классической области, т.е. вне области -a₀ < x < a₀. Значение a₀ находится просто

Найдем сначала вероятность обнаружения частицы в классической области

где y = x/x₀. Поскольку под интегралом находится четная функция переменной y, то

Полученный интеграл называется интегралом вероятностей, значения его для различных значений верхнего предела имеются в таблицах. В нашем случае (интеграл от 0 до 1) P_кл ≈ 0.84. Соответственно, вероятность того, что частица будет обнаружена вне классической области, равна P = 1 - P_кл ≈ 0.16. Очень значительная величина!