
Читайте также:
|
1. Составить опорный план, т.е. начальное приближение.
2. Составить математическую модель исходной прямой и математическую модель двойственной задач.
3. Пользуясь методом наименьшего (наибольшего) элемента и методом потенциалов найти улучшение исходного опорного плана до тех пор, пока он не будет удовлетворять условию оптимальности.
Существует ряд методов построения начального опорного решения, наиболее простым из которых является метод северо-западного угла.
В данном методе запасы очередного по номеру поставщика используются для обеспечения запросов очередных по номеру потребителей до тех пор, пока не будут исчерпаны полностью, после чего используются запасы следующего по номеру поставщика.
Заполнение таблицы транспортной задачи начинается с левого верхнего угла, поэтому и называется метод северо-западного угла.
Метод состоит из ряда однотипных шагов, на каждом из которых, исходя из запасов очередного поставщика и запросов очередного потребителя, заполняется только одна клетка и соответственно исключается из рассмотрения один поставщик или один потребитель.
Пример. Составить опорное решение, используя метод северо-западного угла.
 Решение: 1. Распределяем запасы 1-го поставщика.
Решение: 1. Распределяем запасы 1-го поставщика.
Если запасы первого поставщика больше запросов первого потребителя, то записываем в клетку (1,1) сумму запроса первого потребителя и переходим ко второму потребителю. Если же запасы первого поставщика меньше запросов первого потребителя, то записываем в клетку (1,1) сумму запасов первого поставщика, исключаем из рассмотрения первого поставщика и переходим ко второму поставщику.
Пример: так как его запасы a1 =100 меньше запросов первого потребителя b1 =100, то в клетку (1,1) записываем перевозку x11=100 и исключаем из рассмотрения поставщика.
Определяем оставшиеся неудовлетворенными запросы 1-го потребителя b1= 150-100=50.
| 100было-100надо=0осталось | |||||
| 150надо-100было=50осталось. Осталось удовлетворить запросов на 50 единиц товара |
2. Распределяем запасы 2-го поставщика.
Так как его запасы a2 = 250 больше оставшихся неудовлетворенными запросов 1-го потребителя b1 =50, то в клетку (2,1) записываем перевозку x21 =50 и исключаем из рассмотрения 1-го потребителя.
Определяем оставшиеся запасы 2-го поставщика a2 = a2 — b1 = 250-50=200. Так как оставшиеся запасы 2-го поставщика равны запросам 2-го потребителя, то в клетку (2,2) записываем x22=200 и исключаем по своему усмотрению либо 2-го поставщика, либо 2-го потребителя. В нашем примере мы исключили 2-го поставщика.
Вычисляем оставшиеся неудовлетворенными запросы второго потребителя b2=b2-a2=200-200=0.
| 250-50=200 200-200=0 | |||||
| 150-100-50=0 |
3. Распределяем запасы 3-го поставщика.
Важно! В предыдущем шаге у нас был выбор исключать поставщика или потребителя. Так как мы исключили поставщика, то запросы 2-го потребителя все же остались (хоть и равны нулю).
Мы должны записать оставшиеся запросы равные нулю в клетку (3,2)
Это связано с тем, что если в очередную клетку таблицы (i,j) требуется поставить перевозку, а поставщик с номером i или потребитель с номером j имеет нулевые запасы или запросы, то ставится в клетку перевозка, равная нулю (базисный нуль), и после этого исключается из рассмотрения либо соответствующий поставщик, либо потребитель.
Таким образом, в таблицу заносятся только базисные нули, остальные клетки с нулевыми перевозками остаются пустыми.
Во избежание ошибок после построения начального опорного решения необходимо проверить, что число занятых клеток равно m+n-1 (базисный ноль при этом тоже считается занятой клеткой), и векторы-условий, соответствующие этим клеткам, линейно независимые.
Так как в предыдущем шаге мы исключили из рассмотрения второго поставщика, то в клетку (3,2) записываем x32=0 и исключаем второго потребителя.
Запасы 3-го поставщика не изменились. В клетку (3,3) записываем x33=100 и исключаем третьего потребителя. В клетку (3,4) записываем x34=100. Ввиду того, что наша задача с правильным балансом, запасы всех поставщиков исчерпаны и запросы всех потребителей удовлетворены полностью и одновременно.
| Опорное решение | ||||
4. Проверяем правильность построения опорного решения.
Число занятых клеток должно быть равно N=m(поставщики)+m(потребители) — 1=3+4 — 1=6.
Применяя метод вычеркивания, убеждаемся, что найденное решение является "вычеркиваемым" (звездочкой отмечен базисный нуль).
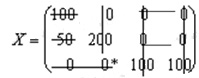
Следовательно, векторы-условий, соответствующие занятым клеткам, линейно независимы и построенное решение действительно является опорным.
Графы. Основные понятия.
Граф - это математическое понятие, которое служит для моделирования связей между объектами. Различают ориентированные и неориентированные графы.
Неориентированным графом G называется пара конечных множеств (V,E), где V - произвольное множество объектов, называемых вершинами и ЕÍ{{i,j}|i,j Î V} множество неупорядоченных пар вершин, где {i,j} Î Е называется ребром.
Ориентированным графам (орграфам) называется пара конечных множеств G’=(V, A), где V -
множество вершин, и AÍ {(i,j)|i,j Î V} множество упорядоченных пар вершин, где АÎ(i,j) – называется дугой. Если i, j – это дуга, то i наз. Непосредственным предшественником j, а j непосредственным последователем i-го.
Количество дуг, входящих в вершину i наз. Степенью захода этой вершины, а кол-во дуг, выходящих из вершины i наз. Степенью исхода из этой вершины. В неориентированном графе вершины i, j наз. Концами ребра. Матрицы смежности графа G(V,E) наз. Матрица А=||а i,j ||n*n c элементами а i,j =1, если {i,j} Î Е и а i,j =0 если {i,j} не принадлежат Е.
Маршрутом в неориентированном графе G наз. Последовательность вершин W=(  ,…
,…  ), n>=0. Граф наз. Связным, если существует маршрут, связывающие любые 2 вершины и маршрут наз. Замкнутым если n>0 и
), n>=0. Граф наз. Связным, если существует маршрут, связывающие любые 2 вершины и маршрут наз. Замкнутым если n>0 и  .
.
Дата добавления: 2015-02-16; просмотров: 187 | Поможем написать вашу работу | Нарушение авторских прав |
|