Читайте также:
|
Глава 2. Матрицы и определители
Матрицы. Действия с матрицами.
Определение. Матрицей называется прямоугольная таблица чисел.
Обозначения: А – матрица, 
- элемент матрицы, 
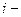номер строки, в которой стоит данный элемент, 
номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.
Определение. Числа m и n называются размерностями матрицы.
Определение. Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы.
Определение. Матрицы одинаковой размерности называются равными, если у них соответственно равны элементы, стоящие на одинаковых местах.
Определение. Матрица называется нулевой, если все ее элементы равны 0.
Виды квадратных матриц
| 1. Верхняя треугольная | 2. Нижняя треугольная |
| 
|
| 3. Диагональная | 4. Единичная |
| 
|
Дата добавления: 2015-02-16; просмотров: 88 | Поможем написать вашу работу | Нарушение авторских прав |