Читайте также:
|
Докажем формулу 
. По определению производной имеем:
Произвольный множитель можно выносить за знак предельного перехода (это известно из свойств предела), поэтому
На этом доказательство первого правила дифференцирования завершено.
Пример.
Найти производную функции 
.
Решение.
Из таблицы производных для тригонометрических функций видим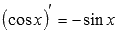 
. Воспользуемся правилом вынесения множителя за знак производной:
Достаточно часто приходится сначала упрощать вид дифференцируемой функции, чтобы воспользоваться таблицей производных и правилами нахождения производных. Следующие примеры это наглядно подтверждают.
Пример.
Выполнить дифференцирование функции 
.
Решение.
По свойствам логарифмической функции можно перейти к записи 
. Осталось вспомнить производную логарифмической функции и вынести постоянный множитель:
Пример.
Найти производную функции 
.
Решение.
Преобразуем исходную функцию 
.
Применяем правило вынесения множителя за знак производной и из таблицы берем производную показательной функции:
К началу страницы
Дата добавления: 2015-01-30; просмотров: 169 | Поможем написать вашу работу | Нарушение авторских прав |