Студопедия
Главная страница | Контакты | Случайная страница

АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Производная частного двух функций (производная дроби).

Читайте также:
  1. А) налоги — объективная необходимость, но их пределы — проблема, поскольку они непосредственно сказываются на эффективности частного бизнеса;
  2. Аппроксимация, интерполяция и экстраполяция функций
  3. Бессознательное как философская проблема. Трактовка генезиса содержания и функций бессознательного в классическом психоанализе.
  4. Бета-каротин («производная» витамина А) противопоказан курильщикам – увеличивает риск заболевания раком легких.
  5. Билет 35. Значение лимбической системы в регуляции различных функций.
  6. В числе функций государственного земельного контроля можно выделить информационную, превентивную, а также функцию пресечения.
  7. Венчурное финансирование частного бизнеса
  8. Вероятности результатов измерения координаты и импульса. Пространство волновых функций.
  9. Взаимосвязь основных и конкретных функций управления
  10. Вид частного решения y* неоднородного уравнения в некоторых конкретных случаях

Докажем правило дифференцирования частного двух функций (дроби) . Стоит оговориться, что g(x) не обращается в ноль ни при каких x из промежутка X.

По определению производной

Пример.

Выполнить дифференцирование функции .

Решение.

Исходная функция представляет собой отношение двух выражений sinx и 2x+1. Применим правило дифференцирования дроби:

Не обойтись без правил дифференцирования суммы и вынесения произвольной постоянной за знак производной:

В заключении, давайте соберем все правила в одном примере.

Пример.

Найти производную функции , где a – положительное действительное число.

Решение.

А теперь по порядку.

Первое слагаемое .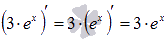

Второе слагаемое

Третье слагаемое

Собираем все вместе:


 

 

 

 

 



Дата добавления: 2015-01-30; просмотров: 149 | Поможем написать вашу работу | Нарушение авторских прав


lektsii.net - Лекции.Нет - 2014-2025 год. (0.007 сек.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав