Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

При делении комплексных чисел их модули, соответственно, делятся, а аргументы, соответственно, вычитаются.

Возведение в степень комплексного числа:

Чтобы комплексное число, заданное в тригонометрической форме, возвести в целую степень, достаточно модуль числа возвести в эту степень, а аргумент умножить на показатель степени:

Zⁿ = |Z |ⁿ (cos n + i sin n ),

Т.е. Zⁿ = |Z |ⁿ = |Z |ⁿ и Arg Zⁿ = n Arg Z

Пример: Найти (-1 +i)⁶ = | 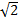(cos + i sin )|⁶ = (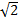)⁶ (cos + i sin ) = 8 | cos ( + ) + i sin ( + )| = 8|cos + i sin | = 8 (0 + 1i) = 8i.

В частном случае при |Z| = 1

(cos + i sin )ⁿ = cos n + i sin n

Извлечение корней из комплексных чисел:

Извлечение корня n-й степени определяется как действие,обратное возведению в натуральную степень.

Корнем n-й степени из комплексного числа z называется комплексное число , удовлетворяющее равенству ⁿ = z, т.е. = , если = z.

Если положить z = r (cos + i sin ), а = (cos + i sin ), то, по определению корня и формуле Муавра, получаем:

Z = ⁿ = (cos n + i sin n )= r(cos + i sin ).

Отсюда имеем = r, n = + 2 k = 0, -1, 1, -2, 2,… То есть = и = (арифметический корень).

Поэтому равенство = принимает вид

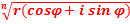= (cos + i sin ), k = 0, 1, …, n-1.

Получим n различных значений корня. При других значениях k, в силу периодичности косинуса и синуса, получается значения корня, совпадающие с уже найденными. Так, при k = n имеем

_n = (cos + i sin ) = (cos ( + 2 ) + i sin ( + 2 )) = (cos + i sin ) = , (k=0).

Для любого z корень n-й степени из числа z имеет ровно n различных значений

14 билет:

Системы двух линейных уравнений с двумя неизвестными имеют вид:

где a, b, c, d, e, f – заданные числа; x, y – неизвестные. Числа a, b, d, e – коэффициенты при неизвестных; c, f – свободные члены. Решение этой системы уравнений может быть найдено двумя основными методами.