Читайте также:
|
---в точке….:
Пусть функции 
и 
удовлетворяют следующим условиям:
1) эти функции дифференцируемы в окрестности точки 
, кроме, может быть, самой точки ;
2) 
и 
в этой окрестности;
3) 
;
4) 
существует конечный или бесконечный.
Тогда существует и 
, причем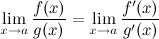 
Вычисление пределов(1й и 2й замечательные пределы)
*Первый замечательный предел:
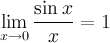
Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.
*Второй замечательный предел:
здесь е - число Эйлера.
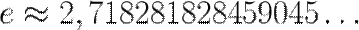
Число е - математическая константа, являющаяся трансцендентным числом. Чаще всего называется числом Эйлера, реже - числом Непера.
Трансцендентное число - это число, которое не может быть корнем полинома с целыми коэффициентами.
Производное(основные понятия, 0 и геометрический смысл)
Производная функции в точке является основным понятием дифференциального исчисления. Она характеризует скорость изменения функции в указанной точке.
Пусть задана некоторая функция . Возьмем какое-нибудь значение 
из области определения этой функции: 
. Соответствующее значение функции в этой точке будет равно 
.
Приращением аргумента называется разность между двумя значениями аргумента: "новым" и "старым".
Обычно обозначается как 
.
Зададим аргументу приращение 
. А тогда значение функции в новой точке 
.
Приращением функции в точке , соответствующее приращению аргумента 
, называется величина:
Производной 
от функции в точке называется предел отношения приращения функции 
к приращению аргумента : 
при 
, если он существует, то есть:
или
Геометрический смысл производной
Производная функции , вычисленная при заданном значении 
, равна тангенсу угла, образованного положительным направлением оси 
и положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой :
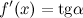
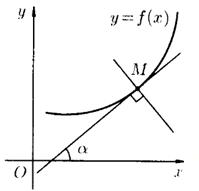
*Геометрически производная представляет собой угловой коэффициент касательной к графику функции в точке .
10) Основные правила дифференциалов и таблица производных:
***********
1. Константу можно выносить за знак дифференциала.
2. Дифференциал суммы/разности.
Дифференциал суммы/разности функций равен суме/разности дифференциалов от каждого из слагаемых.
3. Дифференциал произведения.
4. Дифференциал частного.
5. Дифференциал константы равен нулю.
Таблица производных:
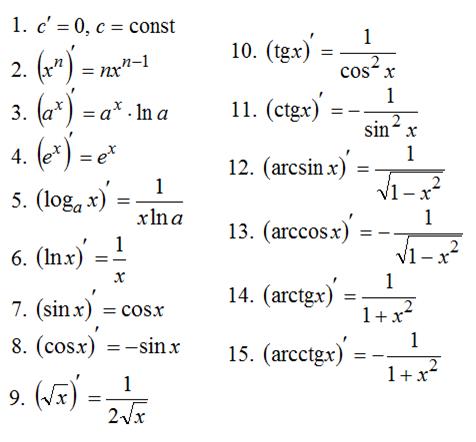
11) Производная не явной функции (производное высших порядков):
Если независимая переменная и функция 
с вязаны уравнением вида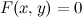 
, которое не разрешено относительно , то функция называется неявной функцией переменной .
Если функция имеет производную в каждой точке своей области определения, то ее производная 
есть функция от . Функция 
, в свою очередь, может иметь производную, которую называют производной второго порядка функции (или второй производной) и обозначают символом 
. Таким образом
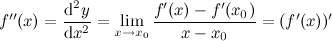
Дата добавления: 2015-02-16; просмотров: 146 | Поможем написать вашу работу | Нарушение авторских прав |