Читайте также:
|
Система линейных уравнений (основные понятия)
Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
Упорядоченный набор значений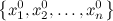 
называется решением системы, при подстановке которых, каждое уравнения обращается в верное равенство.
*СЛАУ называется совместной, если она имеет, хотя бы одно решение.
В противном случае система называется несовместной.
*Система называется определённой, если она совместна и имеет единственное решение.
В противном случае (т.е. если система совместна и имеет более одного решения) система называется неопределённой.
*Система называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно.
*Система называется квадратной, если количество уравнений равно количеству неизвестных.
*Исходную СЛАУ можно записать в матричном виде:
Методы решения систем (Гаусса, Крамара и обратной матрицы)
*Метод Гаусса - классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Для того, чтобы найти решение системы уравнений методом Гаусса и чтобы решение было единственным необходимо, чтобы количество уравнений было равно количеству переменных в системе, то есть необходимо, чтобы система была квадратной.
* Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений (СЛАУ) с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и оно единственно).
При решении СЛАУ методом Крамера используется вычисление определителя. Для того, чтобы систему уравнение можно было решить методом Крамера, необходимо и достаточно, чтобы определитель ее основной матрицы был отличен от нуля, то есть матрица должна быть невырожденной.
* Метод обратной матрицы (Матричный метод) решения систем линейных алгебраических уравнений с ненулевым определителем основной матрицы состоит в поиске матрицы, обратной к основной матрице, и умножению ее на матрицу свободных членов.
При решении систем уравнений методом обратной матрицы используются вычисления определителя матрицы (Для вычисления матрицы, обратной к основной матрице системы уравнений). Для того, чтобы матрица имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля, то есть матрица должна быть невырожденной.
6) Функция (определение и её области)
* Функция - зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. то переменную х называют независимой переменной или аргументом, а переменную у называют зависимой переменной.
Все значения независимой переменной x, образуют область определения функции. Все значения, которые принимает зависимая переменная y, образуют область значений функции.
*Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции, то есть по оси абсцисс откладываются значения переменной x, а по оси ординат откладываются значения переменной y.
7) Предел функции в точке и на бесконечности/ноля
Дата добавления: 2015-02-16; просмотров: 111 | Поможем написать вашу работу | Нарушение авторских прав |
|