Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Необходимое условие экстремума

Теорема 2

(Необходимое условие экстремума)

Если функция имеет экстремум в точке , то ее производная либо равна нулю, либо не существует.

Точки, в которых производная равна нулю: , называются стационарными точками функции.

Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки - это либо стационарные точки (решения уравнения ), либо это точки, в которых производная не существует.

Замечание

Не в каждой своей критической точке функция обязательно имеет максимум или минимум.

Первое достаточное условие экстремума Теорема 2

(Первое достаточное условие экстремума)

Пусть для функции выполнены следующие условия:

1. функция непрерывна в окрестности точки ;

2. или не существует;

3. производная при переходе через точку меняет свой знак.

Тогда в точке 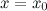функция имеет экстремум, причем это минимум, если при переходе через точку производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку производная меняет свой знак с плюса на минус.

Если производная при переходе через точку не меняет знак, то экстремума в точке 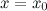нет.

Таким образом, для того чтобы исследовать функцию на экстремум, необходимо:

1. найти производную ;

2. найти критические точки, то есть такие значения , в которых или не существует;

3. исследовать знак производной слева и справа от каждой критической точки;

4. найти значение функции в экстремальных точках.