Читайте также:
|
Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ*, который доставляет минимальное значение f(χ*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации, необходимо задать:
1. Допустимое множество множество 
;
2. Целевую функцию — отображение 
;
3. Критерий поиска (max или min).
Тогда решить задачу 
означает одно из:
1. Показать, что 
.
2. Показать, что целевая функция 
не ограничена снизу.
3. Найти 
.
4. Если 
, то найти 
.
Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек 
таких, что всюду в некоторой их окрестности 
для минимума и 
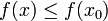для максимума.
Если допустимое множество 
, то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.
Классификация задач оптимизации. (1)
Все задачи оптимизации разбиваются на подклассы в зависимости от условий:
1. Вид функции цели – Fц.
Fц = ax + b. Получаем задачи линейного программирования
Fц = ax2 + bx + c => квадратичное программирование
Fц = a sin(bx) + cedx=> нелинейное программирование.
Если в какой – либо из этих задач функция цели является целочисленной, то мы имеем дело с целочисленным линейным программированием.
2. В зависимости от размерности вектора х: одномерные, многомерные.
3. Количество экстремумов функции цели (Fц): одноэкстремумные задачи и многоэкстремумные задачи.
4. В зависимости от наличия ограничений (если хотя бы одно присутствует – условная оптимизация, если нет – безусловная оптимизация).
Так же задачи оптимизации можно разделить по области их применения: как правило, в экономике и управлении рассматривается задача линейная многомерная с ограничениями; в технических и инженерных имеют место, в основном, нелинейные многомерные задачи с граничными условиями.
Дата добавления: 2015-02-16; просмотров: 82 | Поможем написать вашу работу | Нарушение авторских прав |