Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Доказательство

[править]1. Необходимость

По условию теоремы существует предел

,

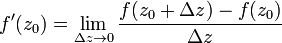не зависящий от способа стремления 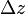к нулю. Положим и рассмотрим выражение

.

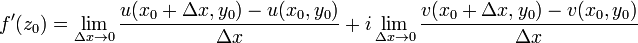Из существования предела комплексного выражения следует существование действительной и мнимой его частей. Поэтому в точке 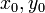существуют частные производные по x функций u(x,y) и v(x,y) и имеет место формула

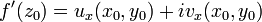
Полагая , находим

.

Сравнивая две последние формулы, убеждаемся в справедливости условий Коши-Римана.

[править]2. Достаточность

По определению дифференцируемости, приращения функци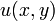й и в окрестности точки могут быть записаны в виде

,

,

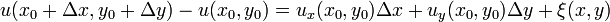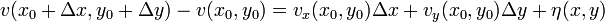где функци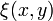и и 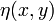стремятся к нулю при , быстрее, чем и 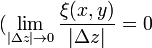, , 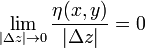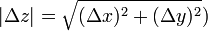. Составим теперь разностное соотношени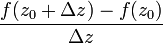е , где 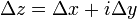и преобразуем его к виду

.

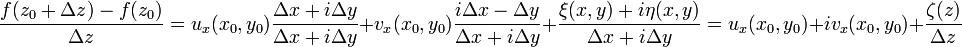
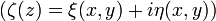Заметим, что при стремлении к нулю последнее слагаемое этой формулы стремится к нулю, а первые остаются неизменными. Поэтому существует предел , что и доказывает дифференцируемость функции в точке .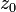

[править]В полярных координатах

В полярной системе координат 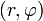условия Коши-Римана выглядят так:

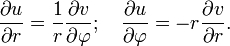
Компактная запись:

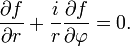
35.